In this article, I will guide you through estimating your required rate of return for stock valuations. Often referred to as the "discount rate," this figure represents the minimum return that an investor seeks to make an investment worthwhile. The discount rate essentially indicates the expected annual return from a stock, derived by discounting the stock's future projected cash flows to their present value. Accurately understanding and estimating this rate for potential stock investments is important, as it is a key input in absolute valuation models.

This article begins with an overview of the required rate of return and then moves to discount rate benchmarks, focusing on U.S. Treasuries and the AAA Corporate Bond Rate. Following this, we'll cover fundamental models such as the Capital Asset Pricing Model (CAPM), Weighted Average Cost of Capital (WACC), and Dividend Discount Models (DDMs). Additionally, we'll explore multifactor models, including the Build-Up Method, Arbitrage Pricing Theory (APT), and the Fama and French Multifactor Models, for alternative discount rate estimations. The article concludes with insights into determining your personal required rate of return.

This comprehensive approach will therefore provide you with a clear understanding of the importance of discount rates, their nuances, and their applications when it comes to stock valuations.

Understanding the Required Rate of Return

The required rate of return (aka discount rate) is an important component in stock valuations, indicating the minimum return an investor seeks from a risky investment. It serves as a benchmark to evaluate the attractiveness of potential investments, with those offering returns below this rate typically seen as unattractive, and those exceeding it considered potentially worthwhile.

The choice of method to estimate this rate is critical, as each method comes with different assumptions and focuses on various aspects of risk and return. Accurate valuation hinges on choosing a method that aligns with an investor's grasp of market dynamics and the specific risks tied to a stock, particularly since valuation models are highly sensitive to the discount rate.

Understanding the inverse relationship between the discount rate and valuation outcomes is also essential:

• Lower Discount Rates --> Higher Valuations: When the discount rate is lower, it generally results in higher valuations of stocks, suggesting that more stocks might be undervalued.
• Higher Discount Rates --> Lower Valuations: Conversely, higher discount rates tend to lead to lower valuations, implying that more stocks might be overvalued.

Applying the discount rate in absolute valuation models involves discounting projected cash flows and the terminal value to their present values, as most commonly represented by the Discounted Cash Flow (DCF) model.

For reference, the DCF intrinsic value formula is shown below:

DCF Intrinsic Value = [FCF₁ / (1+r)¹] + [FCF₂ / (1+r)²] + .... + [FCF_n / (1+r)ⁿ] + [FCF_n * (1+g) / (r - g)]

where:

• FCF = free cash flow
• r = discount rate (required rate of return)
• g = growth rate
• n = time period

Summing the present values of forecasted cash flows and terminal value gives the total intrinsic value of the company, which is then compared to the market value to determine if the stock is overvalued, fairly valued, or undervalued:

• Intrinsic Value < Market Value: Stock may be overvalued, warranting investor caution.
• Intrinsic Value = Market Value: Stock is likely fairly valued, suggesting the market price accurately reflects the company's worth according to the valuation model.
• Intrinsic Value > Market Value: Stock might be undervalued, indicating a possible investment opportunity.

Bottom line, choosing the right method to estimate the required rate of return (aka discount rate), is essential for informed investment valuation decisions. This article offers a thorough examination of various methods, aiming to improve investors' understanding of the risk factors that contribute to estimating the cost of equity (the return investors seek as compensation for the risk associated with stock ownership).

Discount Rate Benchmarks

This section explores the risk-free rate, typically represented by U.S. Treasuries, and compares it with AAA corporate bond rates, highlighting their differing risk profiles and implications for returns in the financial market. Both rates should be thought of as baseline return expectations for any stock market investment.

Risk-Free Rate

The risk-free rate represents the return expected from an investment with zero risk. In practice, U.S. Treasury securities are often used as proxies for this rate, as they are backed by the full faith and credit of the U.S. government, making them as close to risk-free as possible in the financial world.

Investors might opt for different maturities based on their investment horizon. Short-term investors or those seeking a near-term benchmark may lean towards the 3-month Treasury rate. In contrast, long-term investors, especially long-term value investors, often prefer the 10-year Treasury rate, as it aligns well with their typical investment timeline. The 20-year rate could be relevant for very long-term investments or pension funds, where the horizon extends over decades.

The chart below plots the 3-month, 10-year, and 20-year U.S. Treasury rates:

The chart makes it evident that the selected Treasury yield period significantly impacts the baseline expected return. For instance, opting for the 3-month Treasury yield as the risk-free rate in estimating a firm's discount rate would typically result in a lower figure, assuming other factors in the cost of equity model remain constant. This scenario holds true except in unusual circumstances like an inverted yield curve (where short-term interest rates are higher than long-term rates).

Further in this article, we'll cover the various methods for estimating the discount rate, each beginning with the risk-free rate. While the maturity period for this rate might differ, the fundamental concept is that the risk-free rate serves as the primary benchmark. The subsequent approaches we discuss build on this foundational rate by incorporating risk premiums to estimate the cost of equity for stock investments.

Warren Buffett's Preference

Warren Buffett, known as the "Oracle of Omaha," is a world-renowned investor and CEO of Berkshire Hathaway, notable for his exceptional success in value investing.

Based on insights gleaned from Warren Buffett's Berkshire Hathaway Shareholder Letters and Annual Meetings, it's understood that Buffett often references a long-term Treasury rate, such as the U.S. 10-year Treasury rate, as his discount rate.

Below are just two quotes of his that expand upon his discount rate valuation beliefs:

“We don’t discount the future cash flows at 9% or 10%; we use the U.S. treasury rate. We try to deal with things about which we are quite certain. You can’t compensate for risk by using a high discount rate.”

— Warren Buffett | 1998 Berkshire Hathaway Annual Meeting

"And once you've estimated future cash inflows and outflows, what interest rate do you use to discount that number back to arrive at a present value? My own feeling is that the long-term government rate is probably the most appropriate figure for most assets. And when Charlie and I felt subjectively that interest rates were on the low side – we'd probably be less inclined to be willing to sign up for that long-term government rate. We might add a point or two just generally."

— Warren Buffett | 1993 Letter to the Shareholders

These quotes indicate that Buffett prefers a long-term government rate for his discount rate calculations. Notably, in periods of low interest rates, which correspond to lower long-term Treasury rates, Buffett, alongside Charlie Munger, tends to adjust this rate upwards as deemed suitable. This adjustment reflects Buffett's view of the U.S. economy's inclination towards inflation. Further, Buffett does not incorporate a risk premium into his calculations, preferring to avoid additional risks altogether.

To compensate for the implications of using lower discount rates, Buffett employs a significantly large "margin of safety." This approach, in principle, is akin to applying a higher discount rate, such as 10% or more, and then adopting a smaller margin of safety. However, Buffett favors the use of the risk-free 10-year U.S. Treasury rate, making upward adjustments only when interest rates are relatively low. This strategy has proven effective for him, affirming that there's no inherent flaw in adopting such a discount rate methodology.

However, replicating Buffett's approach poses challenges for the individual investor. Adjusting the risk-free rate upwards to reflect Buffett's strategy and accounting for specific company or market insights can still involve moderate uncertainty. Moreover, a significant margin of safety, like over 50%, is expected with a lower discount rate. Estimating this margin across different companies and markets can be somewhat imprecise.

While investors typically seek returns exceeding the U.S. 10-year Treasury rate, precisely pinpointing the achievable rate of return with a substantial margin of safety can be elusive. A clearer approach is to determine the cost of equity either by using one of the methods described in this article or by estimating your own personal required rate of return.

For instance, with Buffett's method, a 4% discount rate (e.g., 3% risk-free rate + 1% adjustment) with a 50% margin of safety might be viable, but it's somewhat vague on the return expected and may overlook other relevant risk premiums. In contrast, using a 12% discount rate plus a margin of safety of 20%, perhaps based on a discount rate model or your own required rate of return, may be more precise and comprehensive.

Bottom line, given the depth of market knowledge required, akin to Warren Buffett's expertise, individual investors might find other methodologies outlined in this article more practical.

• Related: How to Calculate the Intrinsic Value of a Company Like Warren Buffett

AAA Corporate Bond Rate

AAA corporate bonds, rated as the highest quality by credit rating agencies, represent the lowest risk of default among corporate debt investments. This high rating is attributed to assessments of the issuing corporation's financial stability, ability to generate cash flow, and maintain a healthy debt-to-equity ratio, alongside positive future economic prospects. As such, they are often used as a benchmark for safe corporate debt investments.

The yield on AAA corporate bonds reflects not just the bond market's view of corporate health but also broader economic conditions. Typically, these bonds offer lower yields compared to lower-rated bonds, as investors accept lower returns in exchange for higher safety. However, their yields can fluctuate with changes in the economic climate, as they generally decrease during periods of economic uncertainty and increase when the economy is stable.

You can see a chart of the AAA corporate bond yield below:

AAA corporate bonds typically offer higher yields than U.S. Treasuries, compensating investors for the additional risk they carry compared to these government bonds, which are considered virtually risk-free.

Benjamin Graham's Preference

Benjamin Graham, often hailed as the "father of value investing," was a distinguished investor and author, best known for his influential investment philosophies and as the mentor of Warren Buffett.

Unlike Buffett, Graham chose the AAA corporate bond rate as his discount rate for valuing stocks, considering it the minimum acceptable return for such investments. His rationale for this choice was based on the observation that fluctuations in interest rates have a significant impact on the stock market. The yields on AAA corporate bonds, with their high credit rating and relatively low risk, are often viewed as a near risk-free rate for corporate investments. As discussed, AAA corporate bonds carry a baseline level of risk, which typically leads to their yields being higher than those of Treasury bonds.

When applying the AAA corporate bond rate in stock valuations, it's crucial to consider the distinct risk profiles of these bonds versus stocks. Since lower discount rates can lead to higher stock valuations, incorporating a significant margin of safety is prudent. Additionally, it's advisable to add a risk premium to reflect the extra risk and potential returns of stock investments. Stocks inherently pose a greater risk than AAA corporate bonds, so investors should expect correspondingly higher returns.

However, a similar issue arises as with U.S. Treasuries: determining precise risk premiums and an appropriate margin of safety can be quite ambiguous, failing to provide a clear expected rate of return from your chosen discount rate. While the AAA corporate bond rate usually offers a higher yield than U.S. Treasuries, potentially leading to a more conservative valuation model (assuming all other factors are equal), the other methodologies discussed in this article might offer more practicality and clarity, and are therefore worth considering.

• Related: How to Calculate the Intrinsic Value of a Company Like Benjamin Graham

Fundamental Discount Rate Models

Delving into the methodologies of CAPM, DDM, and WACC provides essential insights into their distinct approaches to determining discount rates for stock valuations. Each model offers a unique perspective, from market risk assessment and dividend analysis to a comprehensive view of a company's cost of capital.

Capital Asset Pricing Model (CAPM)

To estimate a company's cost of equity, the widely accepted approach is to utilize the Capital Asset Pricing Model (CAPM). CAPM, a fundamental investment theory, describes the relationship between an investment's expected return and its market risk. Since equity shareholders assume more risk than debt holders, the cost of equity is typically higher, reflecting their need for a higher return to compensate for this additional risk.

The CAPM formula is shown below:

R_e = R_f + β*(R_m - R_f)

where:

• R_e = cost of equity
• R_f = risk-free rate
• β = beta
• R_m = expected market return

Here's an example of the CAPM formula:

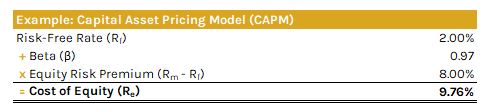
Below are the shortened steps on how to calculate the CAPM:

1. Risk-Free Rate (R_f): Begin by finding the risk-free rate, which is simply the rate on the 10-year Treasury. As we know, this rate is used because it's the interest rate an investor can expect to earn on an investment with zero risk.
2. Stock's Beta (β): Next, find beta, which is a measure of systematic risk (aka undiversifiable risk) of a security or portfolio compared to the overall market (i.e., the S&P 500 Index). By definition, the market has a beta of 1.0. Therefore, betas greater than 1.0 offer higher stock volatility and higher expected returns, while betas lower than 1.0 offer the exact opposite. You can easily find a company's beta on financial websites like Yahoo Finance, or alternatively, calculate it yourself by performing a regression analysis to compare the stock's return volatility with that of the overall market.
3. Expected Market Return (R_m): Finally, we can find the expected return of the market (r_m). For this, you can use analyst estimates of long-term market returns or the historical average market returns. If we are to choose the historical average market returns, from 1926 to 2018 this has been ~10%. Therefore, you can use 10% as the expected return of the market.
4. Solve CAPM Formula (R_e): Solve the CAPM formula with these three inputs to estimate the firm's cost of equity.

For a more comprehensive understanding, you can refer to my article on calculating and interpreting the CAPM.

As a final point, it's important to note that when calculating CAPM for various companies, the distinguishing factor is each company's individual beta, while all other variables in the CAPM formula remain constant. Additionally, if a company does not issue preferred shares (which is common) or has no debt (which is less common), then the CAPM effectively becomes equivalent to the Weighted Average Cost of Capital (WACC), as explained in the following section.

Pros of the CAPM

Below are the key advantages of using the CAPM as the discount rate in stock valuations:

• Diversified Portfolio: CAPM is most suitable for investors who hold a well-diversified portfolio, as it assumes the diversification of unsystematic risk.
• Publicly Traded Stocks: It works best for valuing stocks that are publicly traded in efficient markets, where information is readily available and reflected in stock prices.
• Benchmarking Against Market Returns: Useful for comparing expected returns of a stock to market returns, especially when assessing whether a stock is under or overvalued relative to market risks.
• Long-Term Investments: More appropriate for long-term investment horizons as it is based on the assumption of stable, long-term market risk premiums.
• Risk-Return Analysis: Ideal for situations where the primary focus is on understanding the relationship between expected return and systematic risk of an investment.

In summary, the CAPM is particularly relevant for stock valuations in scenarios involving diversified portfolios and publicly traded stocks in efficient markets. It excels in benchmarking individual stock performance against market returns, making it a valuable tool for assessing whether a stock is valued appropriately in relation to its market risk. CAPM is most effective for long-term investment strategies, as it hinges on the premise of consistent market risk premiums over time. Its core strength lies in analyzing the dynamics between expected returns and the systematic risk associated with a specific investment.

Cons of the CAPM

Below are the key disadvantages of using the CAPM as the discount rate in stock valuations:

• Market Efficiency Assumption: CAPM assumes perfectly efficient markets, which is often not the case in real-world scenarios, leading to inaccuracies in risk assessment.
• Single Factor Model: Relies solely on market risk (beta) to determine expected returns, overlooking other factors such as company size, profitability, momentum, and industry-specific risks that the multifactor models discussed in this article consider. These multifactor models are also proven to better explain market returns.
• Historical Beta Reliance: The model depends on historical data for beta calculation, which may not accurately predict future risks or returns.
• Risk-Free Rate Assumption: Assumes a constant, known risk-free rate, which is not practical given the fluctuating nature of interest rates in the economy.
• Long-Term Orientation: Less effective for short-term investments or in rapidly changing market conditions where the long-term market risk premium assumption does not hold.

In summary, the limitations of the CAPM in stock valuations stem primarily from its reliance on ideal market conditions, like perfect market efficiency and a stable risk-free rate, which are often not reflective of real-world complexities. Its focus on market risk as the sole determinant of expected returns overlooks other influential factors as well. CAPM's dependency on historical beta can lead to inaccurate future risk assessments, and its long-term orientation may not align well with short-term investment strategies or volatile market environments. These constraints suggest that while CAPM can be a useful tool, it should be applied with an understanding of its inherent limitations.

Weighted Average Cost of Capital (WACC)

The Weighted Average Cost of Capital (WACC) is often used as the discount rate in company valuations, offering a comprehensive calculation that includes the cost of debt (from bondholders), the cost of preferred shares (from preferred stock shareholders), and the cost of equity (from common stock shareholders).

The WACC formula is shown below:

WACC = W_d * R_d (1 - T_c) + W_p * R_p + W_e * R_e

where:

• W = weights
• R = cost
• d = debt
• T_c = corporate tax rate
• e = equity
• p = preferred shares

Here's an example of the WACC formula:

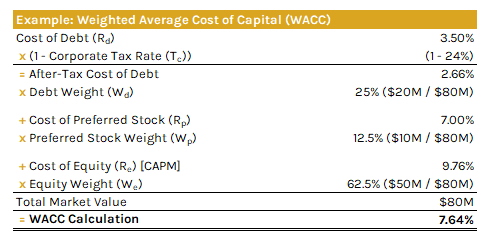
Below are the shortened steps on how to calculate the WACC:

1. Cost of Equity (R_e): The cost of equity is calculated using the Capital Asset Pricing Model (CAPM). As discussed above, this involves finding the risk-free rate (R_f), the stock's beta (β), and the expected market return (R_m).
2. Cost of Debt (R_d): The cost of debt reflects the effective rate a company pays on its borrowed funds. It's computed using either the yield to maturity on existing debt or the interest rate on new debt. The rate is then adjusted to account for the tax shield, acknowledging that interest expenses are tax-deductible.
3. Cost of Preferred Stock (R_p): The cost of preferred stock is determined by dividing the annual preferred dividend by the market price of the preferred stock. This calculation is necessary if the company has issued preferred stock, as it represents the return required by preferred shareholders.
4. Proportion of Debt (W_d), Preferred Stock (W_p), and Equity (W_e) in the Capital Structure: This step requires calculating the market values of equity (E), debt (D), and preferred stock (P). The market value of equity is typically calculated by multiplying the current stock price with the total number of outstanding shares. For the market value of debt, it can be estimated either from the company's balance sheet or from market data if the debt is publicly traded. Similarly, the market value of preferred stock is determined by multiplying its current market price with the number of outstanding shares.
5. Solve WACC Formula: Once the costs of equity, debt, and preferred stock are determined, along with their respective proportions in the capital structure, the WACC can be calculated.

For a more comprehensive understanding, you can refer to my article on calculating and interpreting the WACC.

The WACC is a key indicator used by firms to evaluate the cost-effectiveness of projects and as a discount rate in valuations. It represents the minimum return a company must achieve to satisfy its investors. For instance, if a project is expected to yield a 6% annual return but the company's WACC is 8%, pursuing the project would result in a net loss, effectively eroding the company's value. In such a case, every dollar invested would lead to a loss of $0.02, considering the cost of capital is higher than the returns generated.

A higher WACC indicates a firm with greater downside risk and a higher cost for servicing debt or equity, leading to lower intrinsic value calculations due to the additional return investors demand for increased risk. Conversely, a lower WACC suggests lower risk.

From an investor's standpoint, WACC is commonly used as the discount rate in absolute valuation methods. WACC is preferred as a discount rate as it incorporates stock volatility (beta) and the prevailing interest rate environment from the risk-free rate (such as the 10-year Treasury), along with a market risk premium over the risk-free rate to reflect the higher expected returns from equity investments.

Pros of the WACC

Below are the key advantages of using the WACC as the discount rate in stock valuations:

• Comprehensive Capital Structure Consideration: WACC uniquely accounts for the complete picture of a company's capital structure by incorporating the cost of debt, equity, and preferred stock. This comprehensive approach ensures that all aspects of a company's financing are factored into its valuation, potentially providing a more accurate and holistic understanding of its intrinsic worth.
• Capital Budgeting Decisions: WACC is essential for evaluating new projects within a company, particularly in assessing whether a project's return justifies the overall cost of capital.
• Performance Assessment: It's effective for gauging a company's operational efficiency by comparing the Return on Invested Capital (ROIC) with the WACC, providing insights into how well a company is generating returns relative to its cost of capital.
• Mergers and Acquisitions (M&A): In M&A scenarios, WACC is crucial for evaluating the financial feasibility and potential value creation of these transactions.
• Investment Appraisal: Ideal for assessing investments, especially in situations where a company’s capital structure is stable, and the cost components of capital can be accurately determined.

In summary, WACC is useful in various aspects of stock valuations, including capital budgeting, assessing operational efficiency, facilitating mergers and acquisitions, and conducting investment appraisals. Its comprehensive approach, factoring in debt, equity, and preferred stock, offers a complete view of a company's capital structure.

Cons of the WACC

Below are the key disadvantages of using the WACC as the discount rate in stock valuations:

• Constant Proportions Assumption: WACC assumes a stable capital structure, which can be unrealistic as a company's debt and equity mix may change over time.
• Market Conditions Sensitivity: WACC components are sensitive to market conditions, and fluctuations can lead to significant changes in the calculated WACC.
• Dependence on CAPM for Cost of Equity: As with CAPM's limitations, WACC's accuracy is affected by the assumptions inherent in CAPM, such as market efficiency and a singular focus on market risk.
• Not Suitable for All Companies: WACC may not be appropriate for companies with unusual or complex capital structures or for those in highly volatile industries.

In summary, WACC's reliance on CAPM for the cost of equity brings in limitations associated with CAPM, including a narrow focus on market risk. Its effectiveness is further constrained for companies with unique capital structures or those in volatile industries, where its standard assumptions may not hold. Moreover, WACC's distortions due to the tax shield on debt can complicate its use as a discount rate. While WACC remains a useful tool, these considerations highlight the need for careful application, recognizing its potential for inaccuracies. These concerns are elaborated in my article discussing the flaws of WACC as the discount rate.

Dividend Discount Models (DDMs)

The Dividend Discount Model (DDM) is based on the principle that a stock's value is the present value of its future dividend streams. Therefore, the cost of equity is the discount rate that aligns the stock's current market value with the present value of its dividend payouts. This model is particularly suitable for companies that pay dividends, which are optional distributions some companies make to their shareholders.

Following the DDM principle, various adaptations of the model exist, catering to distinct dividend growth scenarios of companies. Each of these models is capable of calculating the cost of equity, aligning with the specific dividend patterns of the companies being analyzed.

• Gordon Growth Model: Ideal for companies with stable and predictable dividend growth rates, this model assumes that dividends grow at a constant rate indefinitely to calculate the cost of equity.
• H Model: Specifically designed for companies in transition from a high-growth phase to a stable phase, the H Model is useful for companies in more mature stages of their business cycle. It smoothly interpolates between the two stages.
• Two-Stage DDM: Used for companies expected to undergo a phase of rapid dividend growth followed by stable growth. It divides the valuation process into two distinct phases: an initial high-growth period and a subsequent lower, steady-growth period.
• Three-Stage DDM: This model offers a more nuanced valuation process for companies experiencing three phases of dividend growth: a high-growth phase, a transitional phase with declining growth rates, and a final stable growth phase.

The Gordon Growth Model (GGM) can be thought of as the foundational formula of the DDM, as it encapsulates the core principles common to all DDM methodologies. This model simplifies the dividend discount approach by assuming a constant growth rate in dividends, as shown in the formula below:

R_e = [(D₀ * (1 + G)) / P₀] + G

where:

• R_e = cost of equity
• D₀ = most recent dividend payment
• G = constant growth rate in dividends
• P₀ = current stock price

Here's an example of the Gordon Growth DDM formula:

Below are the shortened steps on how to calculate the Gordon Growth DDM:

1. Annual Dividend Growth Rate (G): Project the rate at which dividends are expected to grow annually. This rate can be estimated based on the company's historical dividend growth, industry averages, or expected future earnings growth.
2. Next Year's Dividend (D₀ * (1 + G)): Calculate the expected dividend per share (DPS) for the upcoming year, typically done by multiplying the previous year's dividend (D₀) by one plus the expected annual dividend growth rate (G).
3. Current Share Price (P₀): Obtain the current market price of the stock, which is readily available on financial markets and stock exchange websites.
4. Solve DDM Formula (R_e): Use the DDM formula to calculate the cost of equity. This formula combines the expected dividend per share for the next year, the current share price, and the expected dividend growth rate to estimate the return an investor would require to justify the current stock price.

For a more comprehensive understanding, you can refer to my article on valuing dividend stocks with dividend discount models.

Pros of the DDM

Below are the key advantages of using DDM's as the discount rate in stock valuations:

• Stable Dividend-Paying Companies: DDM is most effective for companies with a history of stable and consistent dividend payments, as it relies heavily on dividends for valuation.
• Mature, Low-Growth Industries: Ideal for companies in mature industries where growth is slow and predictable, and dividends form a significant part of investor returns.
• Income-Oriented Investment Strategies: Suitable for investors focused on dividend income, as DDM provides a direct method to value stocks based on their dividend-paying capabilities.
• Long-Term Investment Horizons: Works well for long-term investment analysis, where the focus is on the sustainability and growth of dividends over time.
• Comparative Analysis: Useful for comparing similar companies within the same industry, particularly when these companies have similar dividend payout patterns.

In summary, the DDM is particularly useful in scenarios where companies have a stable dividend payment history and operate in mature, low-growth industries. It is a preferred method for investors whose primary focus is on dividend income and for long-term valuation purposes. DDM is also beneficial for conducting comparative analyses among similar companies in terms of their dividend distribution patterns.

Cons of the DDM

Below are the key disadvantages of using DDM's as the discount rate in stock valuations:

• Projection of Future Dividend Growth: The model requires projecting future dividend growth, which involves assumptions about the company's cash flows and the proportion of these cash flows paid out as dividends. This adds a layer of uncertainty to the valuation.
• Constant Growth Rate Assumption: DDM assumes dividends grow at a constant rate, an assumption that holds true for some large, stable companies but is unrealistic for many others. This limits its applicability to a narrow range of companies, which is why other more complex DDM's like the H-Model, Two-Stage, and Three-Stage exist.
• Overemphasis on Dividends: The model focuses solely on dividends and overlooks other aspects of a company's financial health and growth prospects, providing a potentially incomplete picture of the company's value.
• Not Suitable for Non-Dividend Paying Companies: DDM is largely inapplicable to companies that do not pay dividends, making it unsuitable for many sectors and growth-focused companies.
• Sensitivity to Dividend Growth Rate Estimations: The model's valuations are highly sensitive to the estimated dividend growth rate. Small changes in this estimate can significantly impact the calculated value.
• Short-Term Market Fluctuations and High Growth Companies: DDM does not effectively account for short-term market volatility and is challenging to apply to high-growth companies where dividends are not a primary focus.

In summary, the DDM, while useful for stable, dividend-paying companies, has significant limitations due to its reliance on assumptions about future dividend growth and the proportion of cash flows paid as dividends. The requirement for dividends to grow at a constant rate further restricts its applicability, making it less suitable for companies that do not fit this profile. These constraints, coupled with its sensitivity to dividend growth rate estimations and its focus solely on dividends, limit the model's overall utility and accuracy, especially for non-dividend-paying and high-growth companies.

Multifactor Discount Rate Models

Exploring multifactor models like the Build-Up Method, Arbitrage Pricing Theory (APT), and Fama-French Models reveals their more complex yet insightful approaches to calculating discount rates. These models incorporate multiple factors, offering a more nuanced and comprehensive analysis of stock valuation beyond single-factor methodologies (like the CAPM).

Build-Up Method

The Build-Up Method is a technique used in stock valuation to estimate the required rate of return, especially for stocks where standard models like CAPM may not fully capture all risk factors. This method is useful in stock valuations as it allows for a more detailed risk assessment by adding specific premiums to the base risk-free rate.

The Build-Up Method formula is shown below:

R_e (Build-Up Method) = R_f = ERP + SRP + IRP + CSRP

where:

• R_e = cost of equity
• R_f​ = risk-free rate
• ERP = equity risk premium
• SRP = size risk premium
• IRP = industry risk premium
• CSRP = company-specific risk premium

Here's an example of the Build-Up Method formula:

Below are the shortened steps on how to calculate the Build-Up Method:

1. Risk-Free Rate (R_f): Identify the yield on long-term government bonds, such as the 10-year or 20-year Treasury bonds, to establish the risk-free rate of return.
2. Equity Risk Premium (ERP): Include the additional return expected for investing in the broader stock market over the risk-free rate. This premium compensates for the general risk associated with the stock market.
3. Size Risk Premium (SRP): Add a premium for the increased risk associated with investing in smaller companies. This reflects the higher volatility and lower liquidity often associated with smaller firms.
4. Industry Risk Premium (IRP): Assess and add a premium specific to the industry in which the company operates. This accounts for the unique risks and volatility characteristics of the particular industry.
5. Company-Specific Risk Premium (CSRP): Include an additional return for unique risks associated with the specific company being evaluated, such as management quality, market position, or financial stability.
6. Solve Build-Up Method Formula (R_e): Sum these four risk premiums to the risk-free rate to solve for the firm's cost of equity.

For a more comprehensive understanding, you can refer to my article on calculating and interpreting the build-up method.

Pros of the Build-Up Method

Below are the key advantages of using the Build-Up Method as the discount rate in stock valuations:

• Detailed Risk Assessment: Allows for a comprehensive analysis of risk by including specific risk premiums like size, industry, and company-specific risks.
• Flexibility: Highly adaptable to different types of stocks and market conditions, providing a more tailored valuation approach.
• Useful for Diverse Companies: Effective in valuing stocks of companies that are not well represented by market indices or do not fit the standard assumptions of models like CAPM.
• Incorporates Industry Dynamics: By including an industry risk premium, it accounts for the unique risks and opportunities within specific sectors.
• Addresses Company-Specific Factors: Allows for the consideration of unique company characteristics, offering a more nuanced understanding of individual stock value.

In summary, the Build-Up Method is advantageous in stock valuations for its detailed and flexible approach to risk assessment. It goes beyond general market risks to include specific factors like industry and company characteristics, making it especially useful for valuing a wide range of companies, including those with unique attributes or operating in specialized industries.

Cons of the Build-Up Method

Below are the key disadvantages of using the Build-Up Method as the discount rate in stock valuations:

• Subjectivity in Risk Premiums: Determining the size, industry, and company-specific premiums involves a degree of subjectivity, which can lead to inconsistencies in valuation.
• Complexity: The method can become complex and time-consuming, especially when assessing multiple risk premiums for accuracy.
• Limited Applicability for Some Companies: May not be as effective for valuing large, diversified corporations where specific risk factors may be less pronounced.
• Data Availability: Accurate valuation depends on the availability of reliable data for each risk premium, which can be challenging, particularly for industry and company-specific risks.
• Potential for Overemphasis on Risk: There's a risk of overstating the overall required rate of return by cumulatively adding multiple risk premiums, potentially leading to undervaluation.

In summary, while the Build-Up Method offers a detailed approach to stock valuation, it faces limitations due to the subjectivity involved in assessing various risk premiums and the complexity of the process. Its applicability may be constrained for certain types of companies, and it depends heavily on the availability of accurate and relevant data. Additionally, there's a risk of overemphasizing certain risks, which could skew the valuation outcome.

Arbitrage Pricing Theory (APT)

The Arbitrage Pricing Theory (APT), introduced by Stephen Ross in 1976, serves as a multifactor alternative to the Capital Asset Pricing Model (CAPM). Unlike CAPM, which uses only the market factor to determine the required rate of return, APT suggests the use of multiple risk factors, such as inflation rates, interest rates, business cycle uncertainty, and others. This allows for a more nuanced approach to risk assessment, capturing the impact of various economic forces on asset returns.

The APT formula is shown below:

R_e = R_f + β_i1*[E(F₁) - R_f] + β_i2*[E(F₂) - R_f] + β_i3*[E(F₃) - R_f] + ... + β_iK*[E(F_k) - R_f] + ε_i​

where:

• R_e = cost of equity
• R_f = risk-free rate
• β_ik = sensitivity of the asset's return to factor k
• E(F_k) = expected return due to factor k
• ε_i = firm-specific or idiosyncratic risk unexplained by macro factors (often omitted in the APT formula)

Here's an example of the APT formula:

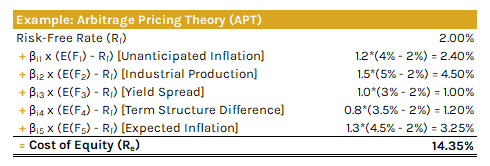
Below are the shortened steps on how to calculate the APT:

1. Risk-Free Rate (R_f): Obtain the yield on long-term government bonds, like the 10-year Treasury bond, to establish the baseline risk-free rate of return.
2. Relevant Risk Factors (F_k): Select economic and other relevant risk factors that influence the asset's performance. Commonly recognized risk factors with statistically significant explanatory powers include macro-economic factors (i.e., inflation rates, interest rates, GDP growth rates), industry-specific factors (i.e., competition and industry growth rates), and company-specific factors (i.e., corporate debt levels, size of the company, return on assets). For the APT model, it's generally advisable to choose a total of 4-5 relevant risk factors.
3. Factor Betas (β_ik): Determine the betas for each chosen factor, which measure the sensitivity of the asset to changes in those specific economic factors.
4. Factor Premiums (E(F_k) - R_f): For each factor, estimate the additional expected return over the risk-free rate. These premiums represent the compensation for the risk associated with each specific factor.
5. Solve APT Formula (R_e): Calculate the expected return of the asset by starting with the risk-free rate and then adding the product of each factor beta with its respective premium.

For a more comprehensive understanding, you can refer to my article on calculating and interpreting the APT.

Pros of the APT

Below are the key advantages of using the APT as the discount rate in stock valuations:

• Multi-Factor Risk Assessment: APT is ideal for valuing stocks where multiple economic factors significantly impact returns, providing a more nuanced risk assessment than single-factor models.
• Diversified Portfolios: It works well for diversified portfolios where specific company risks are less of a concern, and broader economic factors play a more significant role.
• Complex Market Environments: Useful in complex market environments where a variety of economic conditions influence stock performance, offering a more dynamic and adaptable valuation approach.
• Macro-Sensitive Sectors: Particularly applicable for sectors that are highly sensitive to macroeconomic changes, such as finance, energy, or commodities.
• Customizable Analysis: Allows for a tailored approach to valuation by selecting factors that are most relevant to the particular stock or sector.

In summary, the APT shines in scenarios requiring a multifaceted view of risk, particularly when various economic factors drive stock performance. It's well-suited for diversified portfolios and complex market environments, as well as sectors sensitive to macroeconomic shifts. Its customizable nature allows for a tailored analysis, making it a versatile tool in stock valuation.

Cons of the APT

Below are the key disadvantages of using the APT as the discount rate in stock valuations:

• Selection and Estimation of Factors: One of the main challenges is the selection of appropriate factors and accurately estimating their impact, which can be subjective and complex.
• Data Intensity: APT requires extensive data for each factor, which can be difficult to obtain, particularly for more obscure or nuanced economic variables.
• Complexity and Time Consumption: Similarly, the multifactor nature of APT makes it more complex and time-consuming compared to simpler models like CAPM.
• Assumption of Linear Relationships: Assumes a linear relationship between the factors and returns, which may not always hold true in real-world scenarios.
• Sensitivity to Factor Changes: Valuations can be highly sensitive to changes in the chosen factors, making the model somewhat unstable in volatile economic conditions.

In summary, while the APT offers a comprehensive approach to stock valuation, its effectiveness is hampered by the complexities involved in selecting and estimating factors, as well as the extensive data requirements. The assumption of linear relationships and sensitivity to factor changes add to its limitations. Additionally, the complexity and time consumption involved in applying the model can be significant, particularly when compared to simpler, more straightforward valuation methods.

Fama and French Multifactor Models

The Fama and French Multifactor Models, developed by Eugene Fama and Kenneth French, are extensions of the CAPM that introduce additional factors to better explain the risk and return of stocks. The Three Factor Model, introduced in 1992, adds two more factors to the market factor of CAPM: Size and Value. It was developed based on the observation that small-cap stocks tend to outperform large-cap stocks, and value stocks tend to outperform growth stocks. This model aims to explain a significant portion of a diversified stock portfolio’s return relative to the market.

In 2015, Fama and French expanded their model to include two more factors, resulting in the Five Factor Model. This model adds Profitability and Investment as factors, aiming to improve the explanatory power of stock returns. These additional factors help address some of the limitations of the Three Factor Model, though they also introduce new complexities.

The Fama and French Five Factor Model formula is shown below:

R_it - R_ft = α_it + β₁(R_Mt - R_ft) + β₂SMB_t + β₃HML_t + β₄RMW_t + β₅CMA_t + ε_it

where:

• R_it = total return of a stock or portfolio i at time t
• R_ft = risk-free rate of return at time t
• R_Mt = total market portfolio return at time t
• R_it - R_ft = expected excess return
• R_Mt - R_ft = excess return on the market portfolio (index)
• SMB = small minus big (size factor)
• HML = high minus low (value factor)
• RMA = returns spread most profitability firms minus the least profitable (profitability factor)
• CMA = conservatively minus aggressively (investment factor)
• β_1,2,3,4,5 = beta coefficients
• α_it = time regression investment's alpha
• ε_it = time regression residuals

Here's an example of the Fama and French Five Factor Model formula:

Below are the shortened steps on how to calculate the Fama and French Five Factor Model:

1. Risk-Free Rate (R_f): Find the yield on a long-term government bond, like the 10-year Treasury bond, to establish the baseline risk-free rate of return.
2. Market Beta (β_MKT) and Solve CAPM Formula: Determine the stock's market beta, reflecting its market-related volatility, and solve for the CAPM using the inputs previously shown in this article, which includes the risk-free rate and the expected market return.
3. Size Factor Beta (β_SMB): Calculate the beta that reflects the stock's sensitivity to the performance differential between small and large companies.
4. Value Factor Beta (β_HML): Determine the beta indicating the stock's response to the high vs. low book-to-market stocks' performance differential.
5. Profitability Factor Beta (β_RMW): Calculate the beta representing the stock's reaction to differences in company profitability.
6. Investment Factor Beta (β_CMA): Calculate the beta indicating the stock's sensitivity to the investment patterns of firms.
7. Solve Fama and French Five Factor Model Formula (R_e): Combine the results from the CAPM calculation with the additional betas to calculate the stock's expected return using the Fama and French Five Factor Model formula.

For a more comprehensive understanding, you can refer to my article on calculating and interpreting the Fama and French and Carhart Multifactor Models.

Pros of the Fama and French Multifactor Models

Below are the key advantages of using the Fama and French Multifactor Models as the discount rate in stock valuations:

• Comprehensive Risk Factors: Incorporates multiple risk factors, providing a more nuanced and accurate view of risk and return compared to single-factor models like CAPM.
• Empirical Support: Backed by extensive empirical research, showing that size, value, profitability, and investment factors play a significant role in explaining stock returns.
• Flexibility in Application: Adaptable to different market segments and investment styles, making it useful for a wide range of valuation scenarios.
• Enhanced Explanatory Power: Particularly effective in explaining the historical performance of diversified portfolios, offering insights beyond market risk alone.
• Useful for Portfolio Construction: Helps in building and evaluating investment portfolios by considering various dimensions of risk and return.

In summary, the Fama and French Multifactor Models are valuable in stock valuation for their ability to incorporate multiple risk factors, thus offering a more comprehensive risk assessment. Their empirical foundation and flexibility make them suitable for various market segments. These models enhance the understanding of stock returns, particularly for diversified portfolios, and aid in effective portfolio construction and evaluation.

Cons of the Fama and French Multifactor Models

Below are the key disadvantages of using the Fama and French Multifactor Models as the discount rate in stock valuations:

• Complexity: More complex than single-factor models, requiring a deeper understanding and more data for accurate application.
• Estimation Challenges: Determining the appropriate factor premiums and betas can be challenging, potentially leading to inaccuracies.
• Historical Bias: Reliance on historical data for factor premiums might not accurately predict future performance.
• Limited Predictive Power: While explanatory, these models may not always predict future returns effectively, especially in rapidly changing market conditions.
• Potential Overfitting: The risk of overfitting the model to past data, which may not necessarily replicate in future market scenarios.

In summary, the Fama and French Models, despite their comprehensive nature, face limitations due to their complexity and the challenges in estimating factor premiums and betas. The reliance on historical data may not always translate to future market predictability. Additionally, there is a risk of overfitting the models to past data, which may limit their effectiveness in forecasting future stock performance.

Personal Required Rate of Return

The final methodology for estimating the required rate of return (aka discount rate) for a company, and the one I recommend for most investors, is to determine your personal required rate of return for the stock you're evaluating as a potential investment opportunity.

When it comes to determining your required rate of return, investor's should ask: "What is my expected required rate of return from this company each year?" In other words, your discount rate should reflect your personal required rate of return, the annual return you expect from a company's discounted cash flows. This approach is effectively what Buffett, Munger, and Graham do when deciding to buy a company at a specific price, albeit with adjustments upwards from risk-free or near risk-free assets.

Some of the factors that investors should consider when adjusting their personal required rate of return, along with the descriptions for each factors, are shown in the table below:

This rate should be tailored to the specific investment opportunity and will naturally vary among individuals due to differences in risk tolerance, investment objectives, time horizons, available capital, and other personal factors.

For example, if my focus were on mature, slower-growth companies, I'd anticipate a lower annual rate of return, typically in the range of 8-12%. Due to the predictability of their cash flows, I'd also apply a smaller margin of safety in my valuation models. These companies are often preferred by risk-averse or older investors who prefer dividends and/or less volatile returns.

Conversely, for younger or more risk-seeking investors, the attraction often lies in high-growth companies with less predictable future cash flows. In these cases, I would opt for a higher discount rate, about 12-20%. When dealing with stocks perceived as riskier, considering a rate up to 30% would be appropriate to account for the greater uncertainty in their future cash projections. In either case, a relatively large margin of safety would be prudent, reflecting the uncertainty in their future cash flow projections.

If you're unsure about your personal required rate of return, beginning with ~10% (and then adjusting accordingly) is a sensible choice, as it aligns with the market's nominal long-term historical average return. When using this rate in absolute valuation methods, it's ideal to find that your discounted future cash flows yield an "undervalued" assessment. If not, opting for a low-cost broad market index fund might be preferable, as they typically offer more predictable returns than individual stocks. Additionally, considering risk-free assets like U.S. Treasuries, especially when interest rates are favorable and/or confidence in specific stocks or the market is low, may be a smarter choice.

The Bottom Line

In this article, we have thoroughly examined the process of estimating the required rate of return (aka discount rate) for stock valuations. The discount rate is pivotal in absolute valuation models, representing the minimum annual return an investor expects from a stock, and used to discount the stock's projected future cash flows to their present value.

Here's a breakdown of the discount rate methodologies, along with their key merits and drawbacks:

• Discount Rate Benchmarks (U.S. Treasuries and AAA Corporate Bond Rates): These benchmarks provide a baseline for assessing risk-free and low-risk investments, offering a starting point for discount rate estimation. While reliable, they do not fully capture the complexities of individual stock risks.
• Fundamental Discount Rate Models:
  • Capital Asset Pricing Model (CAPM): Offers a straightforward way to factor in market risks but may oversimplify by focusing only on market volatility.
  • Weighted Average Cost of Capital (WACC): Incorporates debt and equity costs, providing a comprehensive view of a company's capital structure but includes the same assumptions as the CAPM, amongst other assumptions.
  • Dividend Discount Models (DDMs): Ideal for dividend-paying stocks, aligning valuation with dividend growth projections, but are less applicable to non-dividend-paying companies.
• Multifactor Discount Rate Models:
  • Build-Up Method: Adds layers of risk premiums for a more tailored approach but requires in-depth market and company knowledge, which can be difficult to come by.
  • Arbitrage Pricing Theory (APT): Allows for multiple risk factors, offering a nuanced view but can be complex and data-intensive. Further, the risk factors were never defined by the original author.
  • Fama and French Multifactor Models: Provides an expanded view of market, size, value, profitability, and investment risks, though their application can have a historical bias.
• Personal Required Rate of Return: The recommended discount rate approach, where you're effectively customizing your personal required rate of return based on the company's relevant risk factors and your individual investment goals. While this approach ensures alignment with your investment strategy, it may introduce subjective biases that could affect objective analysis.

In closing, determining the required rate of return involves a balance between using established financial models and incorporating personal investment criteria. The key is to use these tools judiciously, ensuring that your chosen discount rate accurately reflects both market dynamics and your investment objectives. Lastly, pairing this rate with an appropriate margin of safety and conducting sensitivity analyses further enhances the reliability of your investment valuation models.