In this article, I will show you how to use dividend discount models (DDMs) to value dividend-paying stocks. The premise of DDMs is that stocks can be valued by discounting their expected future dividends to present value, given that expected future stock prices are often influenced by anticipated dividends. DDMs are particularly effective for valuing firms that distribute a substantial portion of their free cash flow as dividends. In these situations, they often provide a more suitable valuation approach compared to other absolute valuation models, such as the discounted cash flow (DCF) model.
This article outlines the overall structure of the DDM, covering its fundamental premise, key inputs essential across all variations, and its strengths and weaknesses as a valuation tool. It will also cover four distinct dividend valuation methods. Although these methods are similar, each is based on unique assumptions about future growth. For each DDM approach, I will discuss its assumptions, relevant applications, and limitations, accompanied by a concise example. This will provide you with a thorough understanding of how to value companies using DDMs.
Dividend Discount Models (DDMs) Explained
When considering cash flows from investments, investors focus on two primary sources:
- Capital Appreciation: This refers to the increase in a stock’s price over the investment period. Investors realize capital appreciation when they sell the stock at a higher price than the purchase price.
- Dividends: These are optional cash payments made to shareholders, representing a portion of the company's earnings.
Given that expected future stock prices are often influenced by anticipated dividends, the premise behind dividend discount models (DDMs) is that a stock's value is equal to the present value of all its expected future dividends, projected indefinitely into the future.
DDMs are designed to encapsulate this concept in their valuation approach. The most general form of the DDM, embodying this core idea, can be expressed by the following formula:
where:
- P0 = stock's fair value value (at time 0)
- E(DPSt) = expected dividends per share (at time t)
- re = discount rate (aka required rate of return)
The DDM model states that the value of an asset is determined by the present value of its expected future dividends, discounted at a rate reflecting the risk associated with these anticipated payments. This approach is based on the time value of money (TVM), which suggests that the current value of money is greater than its future value due to its potential earning capacity. Unlike the discounted cash flow (DCF) model, which focuses on free cash flow (FCF) or owners earnings, the DDM specifically focuses on future expected dividend payments.
Advantages of DDMs
Below is a list of advantages central to all dividend discount models (DDMs):
- Tangible and Objective Valuation: DDMs utilize dividends as actual cash flows, offering a tangible, clear, and objective valuation basis. This approach is less susceptible to the accounting interpretations and non-cash adjustments often associated with earnings. It makes DDMs particularly effective for evaluating companies in mature industries known for consistent dividend payouts. The clarity of dividends as a metric makes them a more accurate and reliable measure of company valuation.
- Conservatism and Stability in Valuation: The emphasis on dividends in DDMs leads to conservative estimates of a company's value, as dividends are generally more stable than earnings or free cash flow. This stability is highly valuable in volatile market conditions and is characteristic of mature, stable businesses. Regular dividend payments signal business maturity and lower risk, often resulting in dividends being discounted at a lower rate compared to other valuation metrics.
- Theoretical Rigor and Reduced Subjectivity: DDMs are grounded in the principle that a company's value equals the present value of all future dividends, offering a theoretically solid foundation with minimal subjectivity. This reduces variability in valuation outcomes among different analysts, as dividends provide a clear, unambiguous metric, contrasting with the more subjective measures of earnings or free cash flow.
- Suitability for Various Investor Profiles: DDMs are particularly suitable for retail investors who lack control over dividend policies and for risk-averse investors who value the predictability and stability dividends offer. They are also crucial for minority shareholders, for whom dividends often represent the only reliable return metric, making DDMs an essential tool in their investment decision-making process.
- Simplicity and Practicality in Application: The simplicity of DDMs, requiring minimal information for calculation, makes them a practical and quick tool for valuation. Although there are nuances, the DDM's rapid application makes it popular as a benchmark or guideline among investors and analysts, especially for those seeking a straightforward method to gauge a company's value.
In summary, DDMs provide a practical, conservative, and theoretically sound method for valuing companies, particularly appealing to investors who prioritize stability and tangible returns. The model's simplicity and objectivity make it a reliable tool for assessing the value of companies with predictable dividend policies.
Disadvantages of DDMs
Below is a list of disadvantages central to all dividend discount models (DDMs):
- Over-Simplification, Limited Scope, and Applicability: DDMs, by focusing mainly on dividends, often exclude unpredictable market activities and company-specific factors like product innovation and growth potential. This limited scope can lead to inaccurate estimates, particularly for companies with sporadic or inconsistently growing dividends. Additionally, DDMs are best suited for mature, stable companies with a consistent dividend history and may not accurately value high-growth companies that reinvest profits instead of paying dividends.
- Sensitivity to Assumptions and Forecasting Challenges: The model is highly sensitive to input assumptions, such as the cost of equity or growth estimates, where minor changes can significantly alter valuations. Forecasting accurate long-term dividend projections is also challenging, and the model does not consider the potential value generated from reinvesting earnings, especially in high-growth firms.
- Disconnection Between Dividends and Earnings: The DDM's assumption that dividends correlate with earnings is often not reflective of real-world practices. Companies might maintain stable dividends irrespective of fluctuating earnings, prioritizing shareholder expectations over actual financial performance. This approach can include instances where companies borrow funds to sustain dividend payouts, thereby creating a significant disconnect between earnings and dividend distributions.
- Tax Efficiency and Shareholder Control Considerations: In countries where dividends are less tax-efficient than capital gains, companies may opt for share repurchases instead, limiting the model's effectiveness. Additionally, the model is less relevant for large shareholders who can influence dividend policies, making it a less useful metric for them.
- Dynamic Business Environments and Dividend Perpetuity Assumption: DDMs assume that companies will pay dividends in perpetuity, which is unrealistic given the dynamic nature of business environments affected by factors like regulation and competition. The model struggles with valuing new companies or startups without a sufficient dividend history and may overestimate values if dividend growth outpaces earnings.
- Contrarian Nature and Market Valuation Discrepancies: The model often misses identifying undervalued stocks in bullish markets due to its exclusive focus on dividends rather than overall market trends. This can lead to overlooking growth opportunities when stock prices rise without a parallel increase in dividends. However, it does adjust valuations in cases where market rises are backed by solid economic fundamentals affecting dividends.
In summary, while DDMs provide a clear and conservative approach to valuing stable, dividend-paying companies, they have several limitations. These include oversimplification, sensitivity to assumptions, limited applicability, challenges in dynamic business environments, and potential discrepancies with market valuations. Therefore, DDMs are most effective when used in conjunction with other valuation methods.
Fundamental Inputs Central to Dividend Discount Models (DDMs)
There are two fundamental inputs in every dividend discount model (DDM): the expected dividends and the discount rate, also known as the "cost of equity" or "required rate of return." These apply to all DDMs, including the four dividend discount valuation methods discussed in this article.
Expected Dividends
In DDMs, expected dividends are estimated by making assumptions about the growth rates of annual dividends per share (DPS) at different stages of a business's lifecycle. More complex DDMs also consider expected earnings per share (EPS), which is the portion of a company's profit allocated to each outstanding share of common stock, and dividend payout ratios (DPR), which are the proportion of earnings paid out as dividends, based on the premise that expected dividends can also be derived by multiplying EPS with DPR.
Now, when discussing expected dividends, a central element in all DDM formulas is the perpetual growth rate at which dividends will grow. There are two fundamental rules investors should always adhere to in this context:
- Growth Rate Must Be Lower Than the Discount Rate: This is crucial because if the dividend growth rate exceeds the discount rate, the dividend would effectively be divided by a negative number, implying a negative value for the company, suggesting it is worthless. Similarly, if the dividend growth rate equals the discount rate, the calculation would involve division by zero, resulting in an undefined value. Both situations are impractical and highlight the importance of maintaining a growth rate that is consistently lower than the discount rate.
- Growth Rate Must Be Below Economic Growth: The perpetual dividend growth rate should be capped at, or slightly above, the economy's growth rate to ensure sustainability and alignment with broader economic conditions. A permissible excess is 1-2% over the economy's gross domestic product (GDP) growth. Additionally, the 10-year U.S. Treasury Note rate can serve as a conservative benchmark, reflecting the minimum risk-free return expected by investors. For multinational companies, it's advisable to consider the global economy's growth rate, potentially combining it with long-term inflation rates for a more holistic approach. This accounts for both economic and inflationary influences on a company's growth.
In addition to adhering to these rules, your perpetual dividend growth rate should be realistic and aligned with the firm's historical growth patterns, and/or expected return on equity (ROE), and dividend payout ratio(s) (DPR).
While historical growth rates can easily be determined using average or compound annual growth rate (CAGR) calculations over a period of time, aligning the perpetual growth rate with the firm's expected ROE and DPR provides to be a more involved process, in which one must calculate the "sustainable dividend growth rate."
The sustainable dividend growth rate formula is shown below:
Sustainable Dividend Growth Rate = ROE * (1 - (DPS / EPS))
where:
- ROE = return on equity (net income / shareholders' equity)
- DPS = annual dividend per share
- EPS = earnings per share ((net income - preferred dividends) / weighted average outstanding shares)
ROE measures how efficiently a company generates profit from shareholder equity, while the DPR shows the proportion of earnings paid as dividends. The sustainable dividend growth formula therefore offers a practical way to determine a company’s potential for increasing dividends without external capital. It incorporates the firm's profitability and dividend distribution, grounded in financial realities, which contrasts with approaches based solely on historical data.
I highly recommend reading my article on how to estimate the perpetual dividend growth rate in dividend discount models, as it offers additional methods, more detail, nuance, and a real-world example on how to properly estimate this growth rate in DDMs.
Discount Rate
The discount rate for a stock is influenced by its perceived riskiness, which varies across different models. Commonly, risk is assessed using the market beta in the Capital Asset Pricing Model (CAPM). More complex approaches, such as the Arbitrage Pricing Theory (APT) and Fama and French Multifactor Models, incorporate various factor betas as well. Alternatively, investors may choose to use their personal required rate of return for the investment under consideration.
Conventionally, the CAPM is associated with dividend discount models (DDMs), so this is the model we'll use in this article for discount rate calculations.
Capital Asset Pricing Model (CAPM)
The Capital Asset Pricing Model (CAPM) explains the correlation between the implied risk of a stock investment and its expected return. According to the CAPM, the higher the implied risk, the greater your expected return.
The CAPM formula is shown below:
re = rf + β*(rm - rf)
where:
- re = cost of equity
- rf = risk-free rate
- β = beta
- rm = expected market return
As shown in the CAPM formula, the expected return from a stock investment is influenced by the risk-free rate (rf) and the market risk premium (rm - rf). This risk premium is adjusted by a factor known as "beta" (β).
This concept is made clear in the CAPM chart illustration below:
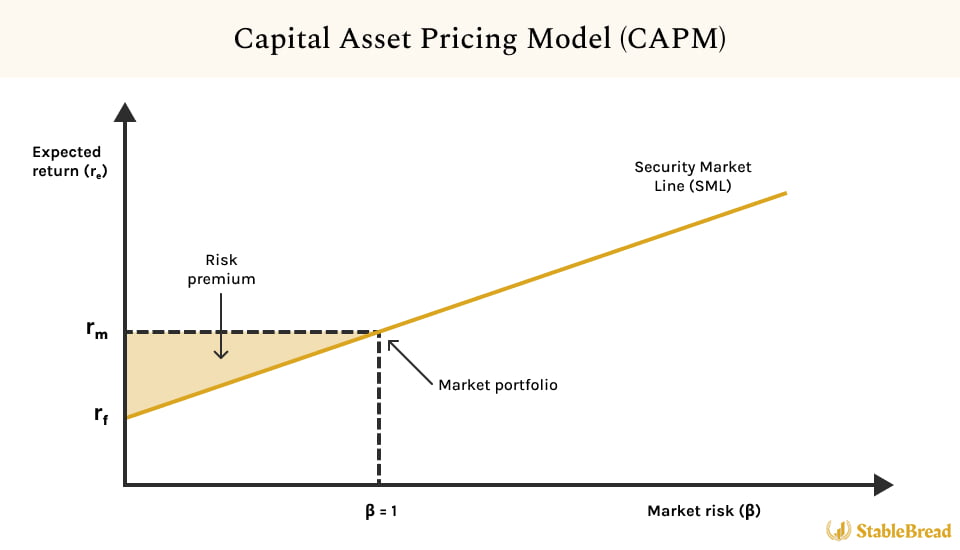
The CAPM chart displays the expected return (re) on the vertical y-axis and beta (β) on the horizontal x-axis. It also shows the Security Market Line (SML), which represents the relationship between beta and the fair value of the expected return for any stock.
To calculate the CAPM for any company, there are only three inputs you have to find/calculate:
- Risk-Free Rate (Rf): Begin with the risk-free rate, typically the yield of the 10-year U.S. Treasury Note. This rate is chosen due to the U.S. government's strong track record of not defaulting on its debt, reflecting a near-zero default risk.
- Beta (β): Find the beta value, which gauges a security's systematic risk relative to the overall market. A beta greater than 1 indicates more volatility compared to the market, while a beta less than 1 shows less volatility. Beta values can be calculated or can be found on financial websites like Yahoo Finance.
- Expected Market Return (Rm): The expected market return often uses a benchmark value of 10%, mirroring the long-term average annual return of broad indices like the S&P 500. This rate is a general indicator of the market's performance over an extended period.
Determining the cost of equity (re) accurately is essential when using dividend discount models (DDMs), given the model's sensitivities to this input. Further, the discount rate in DDMs isn't always constant. In advanced models like the Two-Stage and Three-Stage DDM, the cost of equity changes to match shifts in the company's risk-return dynamics. This usually requires modifying the beta or market risk premium in the CAPM equation to represent these variations correctly.
Gordon Growth Model (GGM)
The Gordon Growth Model (GGM), or constant perpetual growth model, is a basic form of the Dividend Discount Model (DDM). Developed in the 1960's by economist Myron J. Gordon, it assumes dividends will grow indefinitely at a steady state.
The GGM formula is shown below:
where:
- P0 = stock's fair value (at year 0)
- DPS0 = annual dividends per share (at year 0)
- g = perpetual dividend growth rate
- re = discount rate (required rate of return)
The GGM evaluates the present value of an infinite series of dividends growing at a consistent rate. Its calculation requires three key inputs: the current dividend (DPS0), representing the latest dividend payment; the perpetual dividend growth rate (g), the anticipated rate of dividend growth into perpetuity; and the discount rate (re), the minimum expected yield by investors, linked to the stock's risk.
To determine "DPS0," one can refer to a company's financial records or its dividend history. The perpetual dividend growth rate (g) can be derived from historical data, analyst forecasts, or an estimation of sustainable growth, as discussed prior. The discount rate (re), representing the investor's expected return adjusted for risk, is typically calculated using the CAPM.
Zero Growth Dividend Discount Model
The Zero Growth Dividend Discount Model (DDM) offers a slight modification to the GGM, with the sole difference being dividend growth being omitted from the equation. This model can be useful for extremely mature companies in low or no-growth scenarios (e.g., some utilities).
For reference, the Zero Growth DDM formula is shown below:
P0 = DPS0 / re
where:
- P0 = stock's fair value (at year 0)
- DPS0 = annual dividends per share (at year 0)
- re = discount rate (required rate of return)
Clearly, this model is even simpler than the GGM, as you're simply dividing the firm's annual dividends by its expected required rate of return to estimate the firm's fair value.
Assumptions of the GGM
Below are the key assumptions of the GGM:
- Stable Business Model: GGM assumes a company with consistent operations, no major strategic shifts, and a predictable market environment.
- Dividend Policy and FCFE: Assumes that all free cash flow to equity (FCFE) is distributed as dividends, especially relevant for equity-financed firms, linking dividends to company's free cash flow.
- Constant Growth Rate: The model expects a stable growth rate for dividends and FCFE, based on historical trends.
- Stable Financial Leverage: GGM expects unchanged capital structure, ensuring consistent cost of equity and risk profile.
- Perpetual Existence: Assumes the company will continue indefinitely, maintaining its competitive position and profitability.
In summary, the GGM's applicability is anchored in assumptions of stable business operations, consistent dividend policies, constant growth, and perpetual company existence.
Relevant Applications of the GGM
Below are the relevant applications of the GGM based on its assumptions:
- Firms with Stable Growth Rates: Suitable for firms with stable growth rates, typically at or below the economy's nominal rate.
- Firms with High Dividend-Payouts Reflecting FCFE: Ideal for companies where a significant portion of FCFE is distributed as dividends.
- Firms with Stable Leverage: Applicable to companies with consistent leverage ratios.
In terms of ideal industries and candidates:
- Stable Blue-Chip Dividend-Paying Companies: These companies, known for their long-term dividend growth and consistent payouts, embody the stability required by the GGM.
- Real Estate Investment Trusts (REITs): REITs, mandated to pay out 90% of their earnings as dividends, offer the stable, predictable dividend flow that the GGM values.
- Regulated Companies in Utilities and Energy: Operating within specific constraints, these companies' growth often aligns with the economy's rate and features high, stable dividends and leverage.
- Large Financial Service Companies: Their substantial size often limits growth potential, leading to substantial dividends and limited leverage flexibility, making their financial metrics predictable.
- Companies With Established Dividend Policies: Firms with a consistent history of dividend payouts and regular increases fit well within the GGM framework.
In summary, the GGM is most effective for stable, dividend-rich sectors like blue-chip companies, REITs, and regulated utilities, aligning with its growth and dividend assumptions.
Limitations of the GGM
Below are the limitations of the GGM that are specific to its framework:
- Constant Growth Assumption: The steady dividend growth rate assumption may not align with variable growth rates in many companies.
- Input Sensitivity: The model is highly sensitive to growth rate and discount rate, where small changes can significantly alter valuation.
- Limited Applicability for Certain Firms: Less suited for companies with irregular dividends, non-dividend payers, or those preferring reinvestment over dividend distribution.
In summary, the GGM is effective for stable, dividend-paying companies, but its utility is limited by its assumptions and sensitivity to input parameters.
GGM Example
Duke Energy (DUK) operates as a diversified utilities company with a core focus on generating, transmitting, and distributing electricity, as well as providing natural gas services. This is a utilities company that has a long history of paying dividends, at a predictable consistent growth rate, making it a suitable candidate for the GGM.
Below are the GGM inputs determined for Duke Energy:
- DPS0 (TTM) = $4.08 (given)
- g = 2.0% (assumption, based on firm's historical dividend growth rates and sustainable dividend growth rate)
- re (CAPM) = 6.83% (4.22% + 0.45*(10% - 4.22%))
Using these inputs, we can calculate the GGM for Duke Energy:
Solving for Duke Energy's fair/intrinsic value using the GGM yields a value of $86.12 per share. Assuming no additional margin of safety or sensitivity analysis has been conducted, and comparing this figure to the firm's current stock price of ~$98.08, it appears that the stock is currently overvalued.
Two-Stage Dividend Discount Model
The Two-Stage Dividend Discount Model (DDM) is a variant of the DDM tailored for firms experiencing an initial period of extraordinary dividend growth, followed by a transition to steady growth into perpetuity.
The figure below depicts the expected dividend growth over time in the Two-Stage DDM:
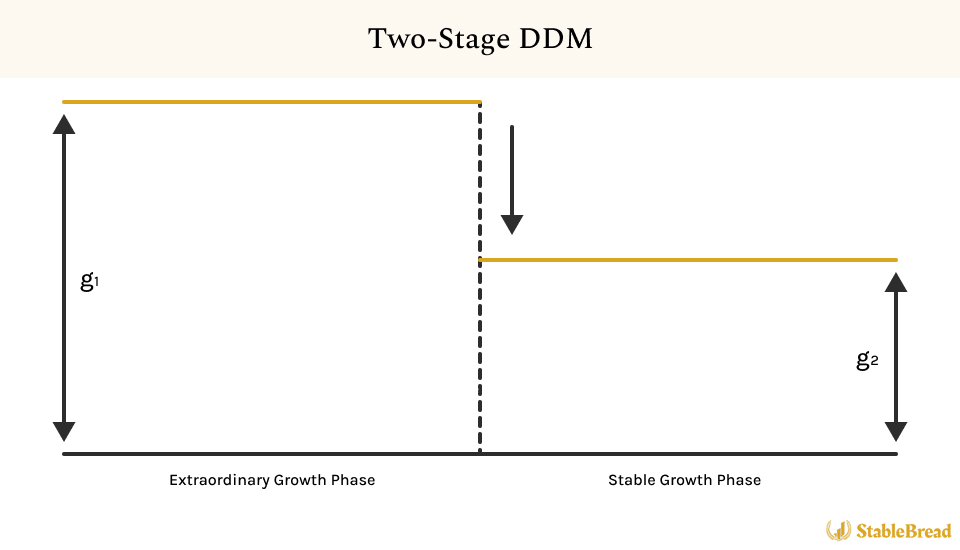
The Two-Stage DDM recognizes two distinct phases of growth: an initial phase marked by irregular and often higher growth rates, driven by rapid expansion or significant market penetration, followed by a second phase in which growth rates stabilize, resulting in consistent and indefinite dividend growth.
While the initial growth rate is usually higher than the perpetual stable rate, it can also be slower or negative. Further, if the initial growth rate aligns with the perpetual growth rate, the Gordon Growth Model (GGM) would be more appropriate.
Below, two Two-Stage DDM formulas are discussed. The key distinction between them rests in the estimation of dividends during the extraordinary growth phase.
Two-Stage DDM Formula: Option #1
The first Two-Stage DDM formula is shown below:
where:
- P0 = stock's fair value (at year 0)
- DPSt = annual dividends per share (in year t)
- n = final year of first-stage dividend growth (i.e., when dividend growth changes from g1 to g2)
- g1 = extraordinary high/low dividend growth rate (first stage)
- g2 = perpetual dividend growth rate (second stage)
- re,1 = first growth period discount rate (aka required rate of return)
- re,2 = stable growth period discount rate (aka required rate of return)
The first Two-Stage DDM formula, also known as the "Variable (Non-Constant) Growth Dividend Discount Model," involves estimating dividend growth for each period of the initial n years in the extraordinary growth phase. The present values of these periods are then calculated and summed to determine the stock's value in this phase. While more intricate, this method could offer a more precise depiction of a stock's intrinsic value, aligning more closely with actual business dividend policies.
Two-Stage DDM Formula: Option #2
Now, if you assume that the extraordinary growth rate (g1) and the dividend payout ratio (DPR) remain constant for the first n years, then you can use the following simplified Two-Stage DDM formula:
where:
- P0 = stock's fair value (at year 0)
- DPS0 = annual dividends per share (at year 0)
- n = final year of first-stage dividend growth (i.e., when dividend growth changes from g1 to g2)
- g1 = extraordinary high/low dividend growth rate (first stage)
- g2 = perpetual dividend growth rate (second stage)
- re,1 = first growth period discount rate (aka required rate of return)
- re,2 = stable growth period discount rate (aka required rate of return)
Unlike option #1, the second Two-Stage DDM formula streamlines the valuation by not requiring annual dividend estimates for the initial n years of the extraordinary growth phase. It presumes that dividends will grow at a constant extraordinary rate during the first stage, suggesting a steady dividend payout ratio. Though theoretically less exact than the first Two-Stage DDM formula, it is more widely used, as it involves fewer estimations and is easier for most investors. This is the formula we'll utilize in this article as well.
To understand the simplified Two-Stage DDM formula further, it's helpful to divide it into its two constituent phases:
- First Phase (Extraordinary Growth Phase): This phase calculates the present value of dividends during the initial growth period using the current dividend (DPS0), projected to grow at an extraordinary rate (g1) for n years. The formula "((1 + g1)n / (1 + re,1)n)" determines the present value proportion of the compounded dividend at the end of n years. Subtracting this from 1 and then multiplying it by the first year's growth-adjusted DPS0 gives the present value of dividends for this phase. The denominator "(re,1 - g1)" reflects the net discount rate, accounting for the difference between the discount rate (re,1) and the growth rate (g1).
- Second Phase (Stable Growth Phase): After year n, the model transitions into a stable growth phase (g2). Here, the discount rate (re,2) may vary from the initial phase, indicative of changes in the risk-return profile. The stage's formula calculates the present value of dividends starting from year n. "DPSn+1" is computed either by multiplying the final first-stage DPS (adjusted at g1) by (1 + g2), or, under the assumption that EPS and DPS grow at a similar rate, by multiplying the first stage's final EPS (also adjusted at g1) by (1 + g2) and then by the expected stable phase DPR. The resulting dividends are discounted to present value using "DPSn+1 / ((re,2 - g2) * (1 + re,1)n)," thus valuing the dividends during the stable growth phase.
Calculating value using a Two-Stage DDM involves discounting dividends from both the extraordinary growth and steady growth phases. Therefore, summing the total present values from both stages yields P0, the stock's estimated fair/intrinsic value.
Assumptions of the Two-Stage DDM
Below are the key assumptions of the Two-Stage DDM:
- Extraordinary Growth Phase: Characterized by high, low, or negative growth rates, reflecting unique company challenges and strategies like expansion or restructuring.
- Transition to Stable Growth: Post extraordinary growth, the company shifts to sustainable growth, aligning with industry and economic averages.
- Variable Dividend Payout Ratio: Changes with growth phase; lower in high growth due to reinvestment, higher in stable growth.
- Adjustment of Firm Characteristics in Stable Phase: Characteristics like beta and return on equity adjust to reflect stability; beta normalizes, and return on equity aligns with stable company levels.
In summary, the Two-Stage DDM's assumptions of a varied growth phase, transition to stability, changing dividend payouts, and adjusted firm characteristics are key for applying it to firms moving from extraordinary to sustainable growth rates.
Relevant Applications of the Two-Stage DDM
Below are the relevant applications of the Two-Stage DDM based on its assumptions:
- Effective for Diverse Growth Phases: Suitable for companies with varied growth patterns, including high-growth firms transitioning to normal rates and those with moderate initial growth.
- Mature Companies With Consistent Dividends: Aligns well with mature companies having a history of consistent dividends and moderate growth, capturing their shift to a stable phase.
- High Dividend Payout Ratios and Residual Cash Flow Distribution: Applicable to firms with high dividend payout ratios distributing substantial residual cash flows as dividends, indicating a move from reinvestment to shareholder distributions.
In summary, the Two-Stage DDM excels in diverse growth scenarios, is ideal for mature companies with stable dividend records, and fits firms with significant dividend distributions, offering objective valuation and stability in dividend policy.
Limitations of the Two-Stage DDM
Below are the limitations of the Two-Stage DDM that are specific to its framework:
- Defining the Length of Extraordinary Growth Phase: Accurately determining the duration of the extraordinary growth phase is complex, introducing uncertainty in valuation due to the model's sensitivity to this period.
- Abrupt Transition to Stable Growth: Assumes an immediate shift from extraordinary to stable growth, which oversimplifies real-world gradual transitions, potentially leading to inaccuracies.
- Predicting Future Dividend Growth: Forecasting dividend growth in the initial high growth stage is challenging, as firms often reinvest earnings rather than pay substantial dividends.
In summary, the Two-Stage DDM is valuable for stocks transitioning from extraordinary to stable growth but faces challenges in defining growth phase lengths, assuming abrupt growth transitions, and accurately predicting future dividends.
Two-Stage DDM Example
American Express (AXP) functions primarily as a multinational financial services corporation, specializing in payment card services and related offerings. Its core operations include providing a range of credit card, charge card, and traveler's check services. With a long history of paying dividends, and considering assumptions of reduced consumer spending in the near future and the possibility that its current high dividend growth rates may not continue, American Express emerges as a suitable candidate for the Two-Stage DDM.
Here's background information for American Express:
- DPS0 (TTM) = $2.32 (given)
- EPS0 (TTM) = $10.68 (given)
- DPR0 = 21.72% ($2.32 / $10.68)
- ROE (TTM) = 29.33% (given)
Here's the Two-Stage DDM assumptions for American Express:
- g1 = 10.0% (assumption, based on the average last five year's of historical dividend growth)
- g2 = 4.0% (assumption, below nominal growth rate of economy and inflation)
- re,1 (CAPM) = 11.33% (4.22% + 1.23*(10% - 4.22%))
- re,2 (CAPM) = 10.58% (4.22% + 1.10*(10% - 4.22%)); lowering beta expectation.
- n = 5 years (speculative assumption, given that the firm's dividends appear sustainable and have room to grow)
- ROE & DPR: Assuming 15.0% ROE in the stable growth phase, which implies the DPR grows to 73.33% (1 - (4.0% / 15.0%)) after 5 years.
Now that we have all the inputs, we can calculate the Two-Stage DDM for American Express. To simplify the calculation, we'll begin by calculating the value of extraordinary growth:
Next, we calculate the value of stable growth. Note, to calculate "DPSn+1" in the numerator we'll grow the EPS and multiply it by the expected stable dividend payout ratio (of 73.33%) to estimate future dividends. The present value of stable growth calculation is shown below:
By adding together the present value of extraordinary growth and the present value of stable growth, we arrive at American Express' fair/intrinsic value as per the Two-Stage DDM, amounting to $127.80 ($11.19 + $116.61). Without further margin of safety or sensitivity analysis, and comparing this to the company's current stock price of ~$180.51, the stock appears to be overvalued.
H-Model
The H-Model, a variation of the Two-Stage DDM presented by Fuller and Hsia in 1984, introduces a gradual change in extraordinary growth during the initial phase, contrasting with the Two-Stage DDM's immediate shift to stable growth. Following this initial period of gradual change, the model transitions into a perpetual stable growth phase.
The figure below depicts the expected dividend growth over time in the H-Model:

In the H-Model, there are two stages. The first is the extraordinary growth phase, which gradually transitions to the second stable growth phase where dividends continue to grow indefinitely. While the H-model typically assumes a gradually declining dividend growth rate in its initial phase, it can be adapted to model an increasing growth rate if that better aligns with a company's expected performance. In either case, the H-Model calculates the present value of dividends in these two growth phases, accommodating the gradual change in dividend rates over time.
The H-Model dividend discount formula is shown below:
where:
- P0 = stock's fair value (at year 0)
- DPS0 = annual dividends per share (at year 0)
- H = half life of anticipated transition period
- g1 = increasing/declining dividend growth rate (first stage)
- g2 = perpetual dividend growth rate (second stage)
- re = discount rate (aka required rate of return)
To understand the H-Model formula further, it's helpful to divide it into its two constituent phases:
- First Phase (Extraordinary Growth Phase): This phase focuses on the early period of extraordinary growth, gradually transitioning to a more stable rate. The initial dividend growth rate (g1) is set based on historical data, analyst estimates, or the expected dividend growth rate (based on the firm's current ROE and DPR). The formula "DPS0 * H * (g1 - g2) / (re - g2)" captures the present value of dividends during this phase. Here, "DPS0" is the current dividend per share, and "H" represents the half-life of the high-growth period. The term "(g1 - g2)" indicates the difference between the initial extraordinary growth rate (g1) and the subsequent stable rate (g2). The discount rate (re), calculated typically using the CAPM, remains consistent across both stages.
- Second Phase (Stable Growth Phase): After the initial transition, the model shifts to a perpetual stable growth phase, represented by "DPS0 * (1 + g2) / (re - g2)," which is effectively just the Gordon Growth Model (GGM). This part of the formula calculates the present value of dividends growing indefinitely at a stable rate (g2). The perpetual dividend growth rate (g2) can be estimated using historical growth, analyst forecasts, or sustainable growth rate estimations, as discussed prior. As mentioned, the discount rate (re) used here is the same as in the first phase, ensuring consistency in the valuation process.
Calculating value using the H-Model involves discounting dividends from both the extraordinary and steady growth phases. Therefore, summing the total present values from both stages yields P0, the stock's estimated fair/intrinsic value.
Assumptions of the H-Model
Below are the key assumptions of the H-Model:
- Extraordinary Growth Phase: Assumes company's earnings and dividends are experiencing an extraordinary growth phase.
- Linear Change in Earnings: Earnings growth is expected to change linearly over a period indicated as 2H.
- Stable Dividend Payout and Cost of Equity: Dividend payout ratio and cost of equity remain constant throughout the transition phase, despite changing growth rates.
- Steady State Growth Post-Transition: Anticipates stable dividend growth indefinitely after the initial declining phase.
In summary, the H-Model is essential for firms transitioning from extraordinary to sustainable growth rates, but may not suit companies with variable growth patterns, changing dividend policies, or fluctuating costs of equity.
Relevant Applications of the H-Model
Below are the relevant applications of the H-Model based on its assumptions:
- Effective for Diverse Growth Phases: Appropriate for businesses with different growth trends, this method is applicable to high-growth companies moving to regular growth rates and those experiencing low/negative initial growth.
- Companies in Transition: Ideal for larger firms transitioning from an extraordinary growth phase to a stable rate, such as those facing diminishing competitive advantages.
- Firms with Temporary Growth Spurts: Suited for companies with temporary growth surges, such as those with new products or first-mover advantages.
- High Growth and High Payout Firms: Best for firms experiencing both high growth and high dividend payout, less suitable for low or no dividend distributing firms.
In summary, the H-Model is highly effective for companies moving from rapid to more sustainable growth rates, particularly in cases of rapid expansion due to specific factors.
Limitations of the H-Model
Below are the limitations of the H-Model that are specific to its framework:
- Rigidity in Growth Rate Change: Assumes a uniform linear change in growth rates (2H), which may not reflect actual dividend patterns with deviations from linear change.
- Constant Payout Ratio and Cost of Equity Assumption: Presumes constant dividend payout ratio and cost of equity during both phases, not accounting for changes companies might make as growth rates decrease.
- Impact of Long Extraordinary Growth Periods: Less effective for prolonged extraordinary growth phases, leading to disparities between initial extraordinary growth and long-term sustainable rates.
In summary, the H-Model faces limitations in handling non-linear growth changes, constant cost of equity and payout ratios, and extended high-growth periods, impacting its real-world applicability.
H-Model Example
3M Company (MMM) operates as a diversified multinational conglomerate with a focus on industrial, worker safety, health care, and consumer goods. Its expansive operations include manufacturing a wide range of products such as adhesives, abrasives, laminates, passive fire protection, personal protective equipment, window films, paint protection films, and orthodontic products. With its long history of paying dividends, coupled with the fact that dividend growth has significantly slowed in recent years, and as a multinational conglomerate where dividends are likely to stabilize (if they haven't already), 3M presents itself as an apt candidate for the H-Model.
Here's background information for 3M Company:
- DPS0 (TTM) = $6.0 (given)
- EPS0 (2022) = $10.21 (given)
- DPR0 = 58.77% (($2.32 / $10.68); this remains constant in the H-Model).
Here's the H-Model assumptions for 3M Company:
- g1 = 8.0% (assumption, based on the 3-year average growth rate from 2018 to 2020)
- g2 = 1.0% (assumption, based on historical growth rates and sustainable/augmented dividend growth calculations (see here for the estimation process))
- re (CAPM) = 9.91% (4.22% + 0.99*(10% - 4.22%))
- H = 4 years ((8 years / 2); speculative assumption, based on the fact that dividend growth was last "high" in 2019, and we expect it to stabilize by 2027).
Now that we have all the inputs, we can calculate the H-Model for 3M Company. To simplify the calculation, we'll begin by calculating the value of extraordinary growth:
Next, we can calculate the value of stable growth:
Summing the present value of extraordinary growth and stable growth gives us 3M Company's intrinsic value according to the H-Model, totaling $95.54 ($18.20 + $77.34). Without additional margin of safety or sensitivity analysis, and in comparison to its current stock price of ~$106.98, the stock seems to be overvalued.
Three-Stage Dividend Discount Model
The Three-Stage Dividend Discount Model (DDM) combines elements from the Two-Stage DDM and the H-Model, making it the most intricate DDM. This model encompasses three distinct growth phases: initial extraordinary growth, a transitional change in growth, and a final phase of stable growth into perpetuity.
The illustration below captures the expected dividend growth over time in the Three-Stage DDM:
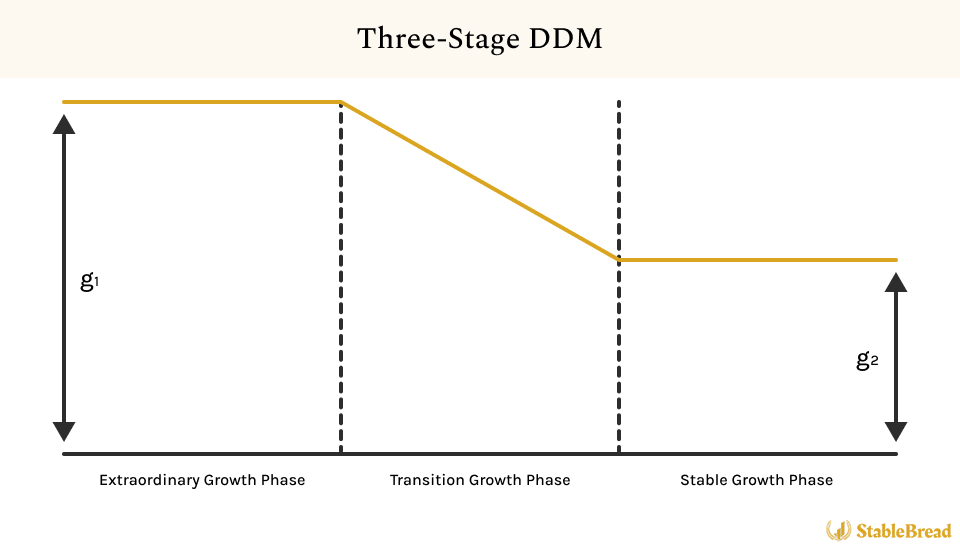
The Three-Stage DDM model outlines three key phases of dividend growth. Initially, there's a high-growth phase driven by aggressive expansion or innovation. This transitions into a phase where dividend growth gradually decreases as the company stabilizes and matures. Finally, a stable growth phase emerges with consistent and predictable dividend increases, reflecting the company's established market position. This model accommodates various growth scenarios throughout a company's lifecycle.
Dividend payout ratios are also expected to vary across these phases. In the high-growth phase, companies retain more earnings for reinvestment, resulting in a lower payout ratio. During the transitional phase, the payout ratio increases as reinvestment needs decline. In the stable growth phase, a high payout ratio is common as companies distribute a significant portion of earnings to shareholders due to limited reinvestment opportunities and secure market positions.
The Three-Stage DDM can be adapted for scenarios where a company initially faces low or negative growth due to market challenges or heavy research and development investments. In such cases, subdued initial growth may precede rapid expansion, leading to a stable growth phase. Consequently, the pattern of dividend payout ratios should be adjusted to reflect this reversed growth trajectory.
Investors can employ two formulas to calculate the Three-Stage DDM and assess a stock's value. The first formula provides a more direct approach, focusing on the present value of expected dividends, suitable for broad analysis. The second formula offers a more detailed analysis, considering variations in earnings and dividend payouts while factoring in changing discount rates across all three phases.
Three-Stage DDM Formula: Option #1
The first formula of the Three-Stage DDM provides a straightforward approach by not incorporating return on equity (ROE) and dividend payout ratio (DPR) expectations, and maintaining a constant discount rate (re). However, it still requires a detailed calculation process.
The first Three-Stage DDM formula is shown below:
where:
- P0 = stock's fair value (at year 0)
- DPS0 = annual dividends per share (at year 0)
- DPSn = expected dividend at the end of the extraordinary growth phase
- n = final year of first-stage dividend growth (i.e., when dividend growth rate changes from g1 to g2)
- H = one-half the duration of the transitional period
- g1 = extraordinary high/low dividend growth rate (first stage)
- g2 = perpetual dividend growth rate (third/final stage)
- re = discount rate (aka required rate of return)
To better understand the simplified Three-Stage DDM formula, let's break it down into its three stages:
- First Phase (Extraordinary Growth Phase): In this initial stage, the focus is on the period of extraordinary growth. Begin with the current dividend (DPS0) and project its growth at an extraordinary rate (g1) for each year until the end of this phase (n years). The present value of each year's dividend is calculated by growing DPS0 by g1 for that year and then discounting it back to the present using the discount rate (re), typically found via the CAPM.
- Transition Phase: This phase deals with the gradual transition from the high initial growth rate (g1) to the more sustainable growth rate (g2). Compute the value of this transition by applying the formula "DPSn * (1 + g2) + DPSn * H * (g1 - g2)," and discount it to the present using the rate "re." "H" here represents half the duration of this transitioning period, serving as an adjustment factor.
- Final Phase (Stable Growth Phase): In this final stage, it's presumed that the company's dividends will increase at a steady rate (g2) indefinitely, aligning with the Gordon Growth Model's principles. The terminal value, determined under this assumption, is then discounted to its present value using the discount rate "re." This reflects the typical expectations for a well-established company in a stable market setting.
Calculating value using the first Three-Stage DDM formula involves discounting dividends from the extraordinary, transition, and steady growth phases. Therefore, summing the total present values from each stage yields P0, the stock's estimated fair/intrinsic value.
Three-Stage DDM Formula: Option #2
The second Three-Stage DDM formula takes a nuanced approach, considering earnings per share (EPS) and the dividend payout ratio (DPR) across different phases. It accommodates distinct payout ratios during the extraordinary growth, transitional, and stable growth phases, reflecting the expected shifts in the proportion of earnings paid as dividends in each phase. This method is particularly valuable when anticipating significant changes in the company's DPR as it progresses through its growth stages. Additionally, this formula utilizes three separate discount rates (re,1, re,2, and re,3), aligning more closely with the evolving risk profile of the company throughout these stages.
The second Three-Stage DDM formula is shown below:
where:
- P0 = stock's fair value (at year 0)
- DPSt = annual dividends per share (in year t)
- EPSt = earnings per share (in year t)
- DPR1 = dividend payout ratio in extraordinary growth phase
- DPR2 = dividend payout ratio in stable growth phase
- n1 = final year of the extraordinary growth phase where the dividend growth rate is g1
- n2 = year when the stable growth rate g2 takes effect after the transition phase
- g1 = extraordinary high/low dividend growth rate (first stage)
- g2 = perpetual dividend growth rate (third/final stage)
- re,1 = discount rate (aka required rate of return) in extraordinary growth phase
- re,2 = discount rate (aka required rate of return) in transition phase
- re,3 = discount rate (aka required rate of return) in stable growth phase
To apply this more intricate Three-Stage DDM formula, let's dissect the valuation process into the respective growth phases:
- First Phase (Extraordinary Growth Phase): During this stage, focus on determining the present value of anticipated dividends derived from earnings per share (EPS). For each year in this extraordinary growth period, project the EPS growth at an accelerated rate (g1), factoring in the dividend payout ratio (DPR1) relevant to this assumed high-growth phase. Then, discount these projected dividends to their present value using a discount rate (re,1) that reflects the increased risk and expected higher returns characteristic of this phase.
- Transition Phase: This stage deals with dividends per share (DPS) in the timeframe between the end of the rapid growth and the onset of stable growth. The present value of these dividends is computed using a transition-specific discount rate (re,2). This phase typically marks a slowdown in growth, representing the company's shift towards a more stable and mature operational phase.
- Final Phase (Stable Growth Phase): Here, calculate the company's terminal value based on the final EPS before the stable phase (EPSn2), projected to grow at a consistent, stable rate (g2). Adjust this value according to the expected dividend payout ratio (DPR2) for the mature phase. The calculated terminal value, assuming ongoing dividend growth at rate g2, is then discounted to present value. This discounting incorporates the initial extraordinary discount rate (re,1), the transition phase rate (re,2), and the final stage discount rate (re,3), capturing the evolving risk profile from the extraordinary growth phase through stability.
Again, calculating value using the more intricate Three-Stage DDM formula involves discounting dividends from the extraordinary, transition, and steady growth phases. Therefore, summing the total present values from each stage yields P0, the stock's estimated fair/intrinsic value.
Assumptions of the Three-Stage DDM
Below are the key assumptions of the Three-Stage DDM:
- Initial Extraordinary Growth Phase With Defined Duration: Begins with high, low, or negative growth due to factors like expansion or restructuring, where defining the duration is crucial for valuation.
- Linear Transition to Stable Growth: Assumes a gradual shift in growth and discount rates, with changing dividend payout ratios, reflecting adjusted risk and reinvestment needs as the company matures.
- Correlation Between Dividend Payout Ratio and Growth Rate: Suggests variable dividend payout ratios depending on growth phases, with higher ratios in stability and lower during high growth.
- Risk Profile, Cost of Capital, and Financial Policy Adjustments: Expects adjustments in risk profile, cost of capital, and financial policies across growth stages, with a decreasing cost of equity moving towards stability.
In summary, the Three-Stage DDM is essential for valuing firms undergoing diverse growth changes, requiring a thorough understanding of its assumptions about growth phases, dividend payouts, risk profiles, and financial policies.
Relevant Applications of the Three-Stage DDM
Below are the relevant applications of the Three-Stage DDM based on its assumptions:
- Dividend Alignment and Initial Extraordinary Growth: Suitable for companies in extraordinary growth phases with dividends closely aligned with free cash flow to equity (FCFE).
- Gradual Growth Rate Decline and Stable Leverage: Excels in capturing gradual growth rate reductions in maturing firms, coupled with stable leverage, reflecting consistent financial strategies.
- Adaptability to Payout and Risk Profile Shifts: Ideal for fast-growing firms undergoing changes in dividend policies and risk profiles, capturing their transition to sustainable growth.
- Realistic Business Lifecycle Representation: Effectively mirrors business cycles, especially for companies initially experiencing high growth due to innovation or market dominance, adapting to their evolving growth dynamics.
In summary, the Three-Stage DDM stands out for its adaptability to diverse growth scenarios, applicability to firms with changing dividend policies, and its ability to reflect shifts in risk profiles and capital structures.
Limitations of the Three-Stage DDM
Below are the limitations of the Three-Stage DDM that are specific to its framework:
- Complexity and Sensitivity in Estimating Inputs: Requires precise estimations of inputs like payout ratios, growth rates, and betas, with sensitivity to these estimates leading to valuation inaccuracies.
- Challenges in Defining Growth Phase Durations: Determining the length of growth phases, particularly the extraordinary growth and transition periods, is challenging and prone to misvaluation due to the difficulty in translating qualitative analyses into exact timeframes.
- Oversimplification of Growth Transition: The assumption of a linear transition from high to stable growth may not reflect the complex and sometimes non-linear nature of real-world growth changes.
- Predicting Future Dividend Growth: Forecasting dividend growth during the early high growth phase can be difficult, since companies typically reinvest profits instead of distributing significant dividends.
In summary, while the Three-Stage DDM is comprehensive and suitable for complex growth patterns, it faces challenges in input estimation, defining growth phase durations, linear growth transition assumptions, and a dividend-centric valuation approach.
Three-Stage DDM Example
Coca-Cola (KO) operates as a leading global beverage company, renowned for its wide array of soft drinks, water, and other beverages. The firm's extensive product portfolio includes famous brands like Coca-Cola, Diet Coke, and Sprite, among others. Despite its consistent dividend payments and EPS growth, there has been an overall slowdown, likely due to its size and dominant market position, which could lead to a decline in growth over time. Additionally, Coca-Cola has a history of disbursing substantial dividends that often align with its free cash flow to equity (FCFE), while maintaining relative financial leverage stability. These factors make Coca-Cola a suitable candidate for the Three-Stage DDM.
Here's background information for Coca-Cola:
- DPS0 (TTM) = $1.84 (given)
- EPS0 (TTM) = $2.49 (given)
- DPR1 = 73.90% ($1.84 / $2.49)
- ROE (TTM) = 38.70% (given)
Here's the Three-Stage DDM assumptions for Coca-Cola:
- g1 = 10.10% (((1 - 73.90%) * (38.70%)); assumption, based on expected growth rate calculation ((1 - DPR) * ROE)))
- g2 = 4.0% (assumption, below nominal growth rate of economy and inflation)
- re,1 (CAPM) = 7.59% (4.22% + 0.58*(10% - 4.22%))
- re,3 (CAPM) = 7.11% (4.22% + 0.50*(10% - 4.22%)); lowering beta expectation.
- n1 = 4 years (speculative assumption, given that the firm's dividends appear sustainable and have some room to grow).
- n2 = 2 years (speculative assumption, given that the firm's dividend growth decline will probably not be too long).
- re,2 = during transition phase, will linearly decline from 7.59% (re,1) in year 4, to 7.11% (re,3) in year 6.
- DPR2 = 80.0% (((1 - (4.0% / 20.0%)); assuming 20.0% ROE in the stable growth phase, which means the DPR1 grows in linear increments from 73.90% to 80.0%).
Now that we have all the inputs, we can calculate the Three-Stage DDM for Coca-Cola. We'll divide the process into three phases: extraordinary growth, transition growth, and stable growth, and then sum up these parts for the final value. An Excel model is recommended for this complex calculation, as doing it manually or with a calculator can be cumbersome.
Present Value of Extraordinary Growth Phase
To begin, we calculate the present value (PV) of extraordinary growth:
DPS & EPS grow by 10.10% annually for 4 years, holding the DPS, DPS & EPS growth rate, DPR1, and discount rate (re,1) constant. Here, DPS is calculated by multiplying EPS with DPR1. PV is calculated using expected dividends divided by one plus the discount rate, raised to the number of periods.
Summing up the first-stage dividends from the table gives us $7.80.
Present Value of Transition Growth Phase
Next, we determine the present value (PV) of transition growth:
Over 2 years, DPS & EPS growth rate and discount rate (re,2) decline linearly, while DPR grows linearly. DPS is still calculated by multiplying EPS with DPR. Unlike the first phase, the cumulated cost of equity method is required for PV calculation due to yearly changes in the discount rate.
Summing this phase's dividends from the table yields $4.21.
Present Value of Stable Growth Phase
Finally, we calculate the present value (PV) of stable growth into perpetuity. While this can't be tabulated due to its indefinite period, here's an illustration for the next five years:
DPS & EPS grow by 4% annually into perpetuity, holding the DPS & EPS growth rate, DPR2, and discount rate (re,3) constant. Here, DPS is calculated by multiplying EPS with DPR1.
The PV of the terminal price would be calculated using the following formula (last part of the Three-Stage DDM formula):
Here's how this calculation would look for Coca-Cola, excluding the PV discounting "(1 + re)n":
For reference, the $4.07 represents the final EPS in the transition phase (year 6). To calculate the terminal price's present value ($108.98), discount it using "(1 + re)n," accounting for the time value of money. This calculation involves dividing $108.98 by the initial discount rate (re,1) and each year's discount rate during the transition phase.
This calculation is shown below for Coca-Cola:
Completing this calculation yields a PV of $70.73 for the stable growth phase.
Calculate Three-Stage DDM and Interpret Results
If we sum the present value of the extraordinary growth phase, transition growth phase, and stable growth phase, we'll get $82.74 ($7.80 + $4.21 + $70.73) as our intrinsic value for Coca-Cola. Without further margin of safety or sensitivity analysis, and comparing this to the company's current stock price of ~$58.60, the stock appears to be undervalued.
The Bottom Line
In assessing the value of dividend-paying stocks, Dividend Discount Models (DDMs) play an important role. The fundamental concept behind DDMs is that a stock's value can be determined by discounting its future dividends to the present value. This approach, rooted in the time value of money, is particularly advantageous for valuing firms with significant and stable dividend distributions. However, DDMs also have drawbacks, including a tendency to oversimplify and a high sensitivity to the assumptions made about future dividend growth and discount rates.
Let's delve deeper into the various forms of DDMs and their specific applications:
- Gordon Growth Model (GGM): This model is best suited for companies exhibiting constant, perpetual dividend growth. GGM calculates the present value of infinite future dividends that grow at a steady rate. While GGM's straightforward approach is beneficial for stable companies, its effectiveness is limited by its reliance on constant growth and discount rate assumptions.
- Zero Growth DDM: This model is tailored for extremely mature companies in environments with little to no growth. It simplifies valuation by dividing the firm’s annual dividends by its expected required rate of return. This model’s primary limitation is its assumption of zero growth, making it unsuitable for companies that are still growing, even modestly.
- Two-Stage DDM (Standard): Designed for companies transitioning from an initial phase of extraordinary growth to a phase of sustainable growth. The Two-Stage DDM captures this shift by first calculating the present value of dividends during the extraordinary growth period and then evaluating dividends in the perpetual growth phase. It's ideal for firms that are expected to experience a significant but temporary period of irregular growth before stabilizing.
- Variable Growth (Non-Constant) Two-Stage DDM: A variant of the Two-Stage DDM, this model allows for varying dividend growth rates during the initial extraordinary growth phase. It requires estimating the dividend growth for each year in this phase, then summing their present values. This approach provides a more detailed valuation for companies whose dividend growth rates are not initially uniform but are expected to eventually stabilize.
- H-Model: An adaptation of the Two-Stage DDM, the H-Model is suitable for companies experiencing a gradual transition from extraordinary to stable growth rates. It calculates the value of dividends during both phases, accommodating the gradual shift in dividend growth rates over time. The model is particularly relevant for firms where the slowdown in growth is expected to be progressive rather than abrupt.
- Three-Stage DDM: The most intricate of the DDMs, it encompasses an initial phase of extraordinary growth, followed by a transitional phase with changing growth rates, and culminating in a stable growth phase. This model is adept at capturing the complex growth patterns of companies that undergo distinct growth phases throughout their lifecycle. It requires careful consideration of the dividend payout ratios and discount rates corresponding to each phase, making it a comprehensive but complex tool for valuation.
Each of these models has its specific strengths and is best applied to companies whose dividend growth patterns align with the model's assumptions. While they provide a structured approach to valuation, their reliability heavily depends on the accuracy of the assumptions regarding dividend growth rates and the choice of discount rates. Investors should use these models as part of a broader analysis, taking into account the dynamic nature of businesses and market conditions.
