In this article, I will show you how to calculate and interpret the Fama and French and Carhart multifactor models. In specific, this refers to the Fama and French Three Factor Model (FFTFM), the Carhart Four Factor Model (CFFM), and the Fama and French Five Factor Model (FFFFM). The purpose of this article is to therefore explain the premise of these models, followed by an example of how to calculate and interpret these models from running a regression on Excel. These multifactor models are important to understand as they better explain the returns on publicly traded stocks, given the addition of other relevant factors that may influence stock market returns.

Prior to multifactor models, finance theory (in the early 1960's) asserted that stock market returns are determined by returns on the market, meaning that stock returns are sensitive and responsive to broader market movements. This is what's referred to as the "Single Index Model" (SIM), as you have the firm's returns which are compared to just one index, being the market index (e.g., the S&P 500 Index).

The single index model is identical to the "Capital Asset Pricing Model" (CAPM), a popular finance model (also from the early 1960's) that attempts to explain the relationship between stock market returns and market risk, by stating that returns on an individual security depends only on its non-diversifiable risk (which is denoted by beta (β)). Unlike the SIM, the CAPM assumes the market is perfectly efficient and no assumption is made that a security's return is linearly dependent on the market return.

What's important here is that the FFTFM (developed in 1992) builds upon the CAPM by including a size and value factor. The FFFFM then goes even further by adding a profitability and investment factor, in an attempt to further explain the drivers of stock market returns. Given this information, this article will provide a brief overview of the CAPM before delving into the Fama and French multifactor models.

Capital Asset Pricing Model (CAPM)

Because the Fama and French multifactor models expand upon the Capital Asset Pricing Model (CAPM) by including additional factors in its discount rate calculation, it's important that you first understand the CAPM and know how to interpret the results of the model's calculation.

Note that the section below is a summary of my more in-depth article on the CAPM, which shows you how to calculate and interpret the CAPM (following a similar format to this article). I highly recommend you read this article (linked below) if you've never heard of the CAPM before. Otherwise, the short summary below should suffice.

• Related: How to Calculate and Interpret the Capital Asset Pricing Model (CAPM)

In short, the CAPM is an investment theory and model of equity valuation that was proposed by William Sharpe (1964), John Litner (1965), Jack Treynor (1961, 1962), and Jan Mossin (1966), and builds on the "model of portfolio choice" created by Harry Markowitz (1959) (source). The CAPM was proposed by its founders to better explain the relationship between the expected return of a stock market investment and market risk.

The CAPM formula is below:

E(R_i) = R_f + β_i(E(R_m) - R_f)

where:

• E(R_i) = capital asset expected return
• E(R_m) = expected market return
• R_f = risk-free rate of return
• β_i = investment beta

According to the CAPM, the expected return that you can generate from a stock investment depends on the risk-free rate (R_f) and the market risk premium (R_m - R_f), which is scaled by a factor called "beta" (β). This concept is illustrated in the CAPM chart below:

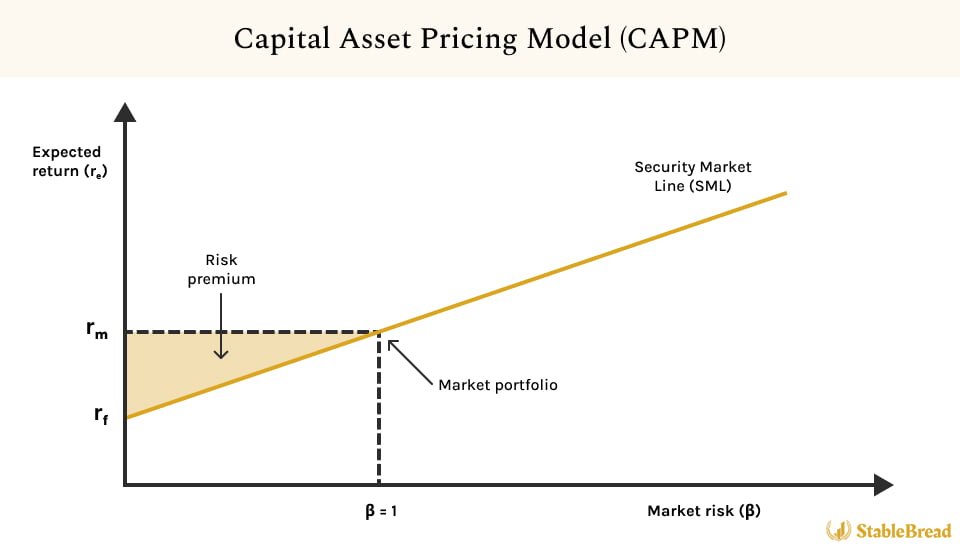
As the CAPM chart above shows, the expected return (E(R_i)) is on the vertical y-axis and the beta on the horizontal x-axis. According to the CAPM model, SML stands for "security market line" and describes the relationship between beta (β) and the fair value expected return for any stock.

There are only three unique inputs in the CAPM calculation (R_f, R_m, and β). Below are the steps on how to find the CAPM for any given publicly traded company. For our simple example, we'll use Target Corporation (TGT), one of the largest retailers in the U.S.:

• Step #1 - Find the Risk-Free Rate (R_f): Begin by finding the risk-free rate, which is simply the rate on the 10-year Treasury Note. This rate is used because it's the interest rate an investor can expect to earn on an investment with practically "zero" risk. As of initial writing, the risk-free rate is 2.67%.
• Step #2 - Find Beta (β): Next, find beta, which is a measure of systematic risk (aka non-diversifiable risk) of a security or portfolio compared to the overall market (e.g., the S&P 500 Index). By definition, the market has a beta of 1.0. Therefore, betas greater than 1.0 offer higher stock volatility and higher expected returns, while betas lower than 1.0 offer the exact opposite. For Target, you can use a site like Yahoo Finance to find their beta (5-yr monthly) of 1.0.
• Step #3 - Find the Expected Return of the Market (R_m): Finally, we can find the expected return of the market. For this, you can use analyst estimates of long-term market returns or the historical average market returns. If we are to choose the historical average market returns, from 1926 to 2018 this has been approximately 10-11%. Therefore, you can be conservative and use 10% as the expected annual return of the market.
• Step #4 - Solve for Target's CAPM (E(R_i)): Putting this altogether gives us Target's cost of equity of 10% (2.67% + 1.0*(10% - 2.67%)). As you can see, this is equal to the expected return of the market, given that beta for this company is equal to one.

To interpret the CAPM, investors can regress the firm's returns onto returns of the market index, adjusted for the risk-free rate. After running this regression, investors will find "alpha," the abnormal rate of return on a security or portfolio that exceeds what the CAPM predicted or expected in its valuation model. If this alpha is statistically significant (meaning p-value < 5%), then this indicates that by purchasing the stock, there's excess return an investor should expect over simply buying the market (e.g., via the SPY).

However, this can be very misleading due to assumptions and simplifications the CAPM has. These are summarized below:

• Flaw #1 - Risk-Free Rate: The CAPM makes the assumption that investors can borrow and lend at the same rate at the risk-free rate, which is clearly untrue. Additionally, no investment is completely "risk-free" and the 10-year U.S. Treasury rate or short-term T-bill rates are the most applicable proxies to represent a risk-free investment.
• Flaw #2 - Beta: Beta is the only risk-factor in the CAPM, which just compares the volatility of a given stock to the overall market. It can be argued that stock price volatility is not a form of risk. It's also questionable to evaluate the future performance of a stock based on its past volatility relative to the market, especially given the unexpected predictability of stock price movements. Even so, as an investor, you probably wouldn't base a stock market investment decision on one risk-factor, which is the main downside to the CAPM.
• Flaw #3 - CAPM Assumptions: The CAPM is widely used in finance given its simplicity and use in building models. However, given the CAPM's simplicity, it inherently comes with a number of assumptions that are oversimplifications of reality and clearly false. For example, the assumption that the market is always competitive and efficient, and that any relevant company information is readily available and quickly absorbed by all market participants is clearly untrue. Additionally, not all investors are rational and naturally risk-averse, which the CAPM suggests.

In short, the CAPM is a relatively useful and simple model to calculate the cost of equity of a potential investment opportunity. However, given the assumptions the model carries and with beta as the model's only risk-factor, the CAPM falls short in accurately describing the expected returns of a stock market investment. In specific, the CAPM is said to explain roughly 70% of a properly diversified stock portfolio's return versus the market as a whole. Fortunately, this is where other multifactor models play a role by expanding on the CAPM to help further explain the drivers of stock market returns.

Fama and French Three Factor Model

Now that we understand how to interpret and calculate the CAPM, we can discuss the Fama and French Three Factor Model (FFTFM), which asserts that other risk factors could drive stock market returns. This model was invented by Nobel prize winner Kenneth French and Eugene Fama in 1992 and builds upon the first factor in the CAPM, the expected market return, by adding two additional factors: value and size. The two founders backtested thousands of random stock portfolios and uncovered two items from their research:

1. Value Factor: Value stocks (high book-to-market firms) tend to outperform growth stocks (low book-to-market firms), and value stocks are undervalued compared to growth stocks.
2. Size Factor: Small-cap stocks tend to outperform large-cap stocks, and are inherently riskier than large-cap stocks.

To reiterate, Fama and French put forth the argument that over the long-term, returns are higher on smaller firms versus large firms, as well as higher on value (high book-to-market) firms versus growth (low book-to-market) firms. Fama and French also suggested that when you combine value and size with the market factor, this could explain roughly 90% of a properly diversified stock portfolio's return versus the market as a whole. Therefore, the FFTFM theoretically provides a more accurate approach of estimating the discount rate of a publicly traded company, given that it has an additional two risk factors over the CAPM, which only considers beta as its risk factor.

Note that the original study for this model focused on the U.S. stock market, but applications of this model in other countries has shown that the model is fairly sufficient in explaining stock market returns outside of the U.S. as well.

The Fama and French Three Factor Model formula is shown below:

R_it - R_ft = α_it + β₁(R_Mt - R_ft) + β₂SMB_t + β₃HML_t + ε_it

where:

• R_it = total return of a stock or portfolio i at time t
• R_ft = risk-free rate of return at time t
• R_Mt = total market portfolio return at time t
• R_it - R_ft = expected excess return
• R_Mt - R_ft = excess return on the market portfolio (index)
• SMB = small minus big (size factor)
• HML = high minus low (value factor)
• β_1,2,3 = beta coefficients
• α_it = time regression investment's alpha
• ε_it = time regression residuals

As you can see, the FFTFM asserts that a firm's returns are going to be a function of broader market movements (β₁(R_Mt - R_ft)), the movements of small firms vs large firms (β₂SMB_t), and the movements of high valued firms versus low valued firms (β₃HML_t).

The intercept term, α, represents alpha (specifically the "three-factor alpha"), which is the abnormal performance of the asset after controlling for its exposure to the market, firm size, and book-to-market factors. As long as the market is in equilibrium, the intercept should be equal to zero, assuming the three factors adequately capture all systematic risks. If not, whatever this model does not capture will be absorbed into the firm's alpha (or residuals, as discussed below), which will indicate a persistent firm-specific factor that investors are looking for. Regardless, alpha should move towards zero over time, because arbitrager's in the market are going to arbitrage-away the alpha that may otherwise exist.

The residuals in this formula can also sometimes give rise to "idiosyncratic volatility," which represents random movements of the firm on any individual day that cannot be explained by the asset-pricing model. The idiosyncratic volatility should then be consistent with the standard deviation of these residuals (e.g., high idiosyncratic volatility could express greater degree of risk). When looking at idiosyncratic volatility, your concern should be with how firms rank against one another, rather than the absolute value of this volatility.

To further understand the three risk factors of the FFTFM (market, size, and value), see the sections below.

Factor #1: Excess Market Returns

Excess market returns refers to the "(R_Mt - R_ft)" in the CAPM formula and is often called the "market risk premium." This represents the difference between the expected market returns and the risk-free rate.

The excess market return concept is summarized in the bullet points below:

• Equities are riskier than fixed income.
• Equities historically provide a higher rate of return than fixed income.

Market returns (R_Mt) can be represented by an equally-weighted index or a value-weighted index. The most common proxy for this risk factor is the S&P 500 Index (SPX), which as we found before on a historical basis, returns about 10% annually. Depending on the context of the company you're evaluating, there's no issue with using other indices as well. The only caution here is to avoid using a price-weighted index such as the Dow Jones Industrial Average (DJIA), otherwise you'll be using a low-quality factor proxy in your regression that can provide misleading appearances of alpha.

Factor #2: Size of Firms

The firm size factor, also known as SMB (small minus big) is equal to the difference in returns between portfolios of small and big firms. Even in a risk-adjusted environment, Fama and French found that small firms tend to outperform large firms.

The SMB concept is summarized in the bullet points below:

• Small-cap firms are riskier than large-cap firms.
• Small-cap firms historically provide a higher return than large-cap firms.

For reference, here's also how Fama and French themselves describe the SMB factor:

"SMB (Small Minus Big) is the average return on the three small portfolios minus the average return on the three big portfolios."

- Fama and French (source)

The concept of "size" is typically measured in terms of market capitalization. The market capitalization formula for any given publicly traded company is shown below:

Market capitalization = Current stock price * Total number of outstanding shares

In theory, you could also measure size in terms of assets or shareholders' equity, but this would be a non-standard approach, so I would generally not recommend it.

Factor #3: Book-to-Market Value

The book-to-market value factor, also known as HML (high minus low) is equal to the difference in returns between portfolios of high and low book-to-market firm. This is where Fama and French found that value stocks tend to outperform growth stocks.

The HML concept is summarized in the bullet points below:

• High book-to-market (value) stocks are riskier than low book-to-market (growth) stocks.
• High book-to-market (value) stocks historically provider higher return than low book-to-market (growth) stocks.

For reference, here's also how Fama and French themselves describe the HML factor:

"HML (High Minus Low) is the average return on the two value portfolios minus the average return on the two growth portfolios."

- Fama and French (source)

For reference, the book-to-market ratio formula is shown below:

Book-to-market ratio = Shareholders' equity / Market capitalization

"Book value" (aka shareholders' equity) is simply equal to assets minus liabilities from a company's balance sheet. Clearly, higher book-to-market ratios means the stock is more undervalued and more likely to be considered a value stock, given that it's trading at a cheaper price in the market relative to its book value.

In theory, investors could also look at valuations from a market-to-book-assets perspective, but this likely does not make much of a difference in your final regression output, so I would just stick with the formula above.

Limitations to the Fama and French Three Factor Model

The primary limitation/downside of the FFTFM is that there are still other factors that might be relevant to the explaining stock returns. Specifically, this refers to the alpha that results from the regression output, which is only as good as your benchmarks. To elaborate, this model deems there to be only three factors that can influence stock returns, but if there are additional factors that should be considered (e.g., momentum, profitability, investment, etc.), then your alpha (if statistically significant) is going to be misleading.

There are also some other more firm-specific issues that can arise as well. For example, if you're estimating this model on a firm that has "thin trading," which means it's traded infrequently, you can end up with very biased coefficients (e.g., biased alphas and betas). This can arise simply because the firm hasn't been traded frequently. As a result, you must bear in mind the characteristics of the firm's returns when running a regression.

Regardless, this model gives an idea of the sensitivity of the firm's returns to these factors, and an idea of what the alpha might be. Now, to theoretically improve on the FFTFM, one can look into the Carhart Four Factor Model (CFFM) and the Fama and French Five Factor Model (FFFFM), which include additional risk factors to more accurately portray alpha, as discussed below.

Carhart Four Factor Model

In 1997, Mark Cahart proposed the Carhart Four Factor Model (CFFM), which is simply the Fama and French Three Factor Model (FFFTM) with a momentum factor added. This factor is also referred to as the "monthly momentum factor" (MOM) or the "up-minus-down" (UMD) factor.

In relation to the stock market, momentum is the speed or velocity in which prices change in a publicly tradable security. The momentum factor is found by taking the returns on the positive advancing firms (meaning positive momentum) minus the returns on the negative advancing firms (meaning negative momentum). Therefore, the momentum factor compares the performance of high-momentum firms to low-momentum firms.

The Carhart Four Factor Model formula is shown below:

R_it - R_ft = α_it + β₁(R_Mt - R_ft) + β₂SMB_t + β₃HML_t + β₄MOM_t + ε_it

where:

• R_it = total return of a stock or portfolio i at time t (aka cost of equity)
• R_ft = risk-free rate of return at time t
• R_Mt = total market portfolio return at time t
• R_it - R_ft = expected excess return
• R_Mt - R_ft = excess return on the market portfolio (index)
• SMB = small minus big (size factor)
• HML = high minus low (value factor)
• MOM = momentum factor
• β_1,2,3,4 = beta coefficients
• α_it = time regression investment's alpha
• ε_it = time regression output

Again, alpha (specifically, the "four-factor alpha") represents performance not attributable to any of the four factors. Investors seek positive alpha because it measures the degree at which a firm is performing compared to what you'd expect based on the firms exposure to these other factors. If momentum is an important driver of stock returns and you've omitted this from the model, then you'll end up with a misleading alpha, which could be the case with the FFTFM.

The momentum factor can be calculated by taking the return of the equal weighted average of the 30% highest performing stocks minus the return of the equal weighted average of the 30% lowest performing stocks. This calculation should capture momentum (i.e., the performance of those firms) and can also be captured over different time horizons (e.g., daily, weekly, monthly), depending on how you want to express momentum.

Separately, here's also how Fama and French themselves describe the MOM factor:

"Mom is the average return on the two high prior return portfolios minus the average return on the two low prior return portfolios."

- Fama and French (source)

Now, when you combine the market, value, and size factors with the momentum factor, this could explain roughly 95% of a properly diversified stock portfolio's return versus the market as a whole. Therefore, the CFFM can provide a small improvement in the explanatory power of stock market returns when compared to the FFTFM.

Limitations to the Carhart Four Factor Model

Like the FFTFM, the CFFM is also susceptible to misrepresenting the alpha in a regression output, due to the possibility of other factors influencing this alpha. The application on thin trading also applies to this model as well.

One viable argument against Carhart's momentum factor stems from the model's behavioral-based approach to explaining stock returns. This is unlike risk factors such as SMB or HML as they're more evidence-based and tied to the efficient market hypothesis (EMH). Therefore, although the momentum factor is real, it's difficult to explain.

Fama and French Five Factor Model

In 2015, after many alterations from other finance professionals and researchers to the original Fama and French Three Factor Model (FFTFM) published in 1992, Fama and French updated their original model by adding two additional factors to further improve the explanatory power of stock market returns. Instead of the momentum factor, which Mark Cahart proposed, the Fama and French Five Factor Model (FFFFM) introduced the profitability (RMW) and investment (CMA) factors.

In short, this model was proposed after evidence showed the founders that the FFTFM often overlooked the variation in average returns related to the profitability and investment factors. Therefore, Fama and French came to the conclusion that their original model was an inadequate explanatory model for stock returns, and created the FFFFM as a result.

The Fama and French Five Factor Model formula is shown below:

R_it - R_ft = α_it + β₁(R_Mt - R_ft) + β₂SMB_t + β₃HML_t + β₄RMW_t + β₅CMA_t + ε_it

where:

• R_it = total return of a stock or portfolio i at time t
• R_ft = risk-free rate of return at time t
• R_Mt = total market portfolio return at time t
• R_it - R_ft = expected excess return
• R_Mt - R_ft = excess return on the market portfolio (index)
• SMB = small minus big (size factor)
• HML = high minus low (value factor)
• RMA = returns spread most profitability firms minus the least profitable (profitability factor)
• CMA = conservatively minus aggressively (investment factor)
• β_1,2,3,4,5 = beta coefficients
• α_it = time regression investment's alpha
• ε_it = time regression residuals

Continuing from the discussion on the FFTFM, these two factors are described below.

Factor #4: Profitability

The profitability factor, also known as "robust minus weak" (RMW) is the difference between the returns of firms with robust (high) and weak (low/negative) operating profitability. Therefore, this factor suggests that stocks with a greater operating profitability perform better than less profitable stocks.

For reference, here's also how Fama and French themselves describe the RMW factor:

"RMW (Robust Minus Weak) is the average return on the two robust operating profitability portfolios minus the average return on the two weak operating profitability portfolios."

- Fama and French (source)

Factor #5: Investment

The investment factor, also known as "conservative minus aggressive" (CMA) is the difference between the returns of firms that invest conservatively and firms that invest aggressively. Therefore, this factor suggests that stocks with greater total asset growth have below average returns. Put differently, the CMA factor describes the difference between companies that require little ongoing capital investment to maintain and grow their company and companies that require large ongoing capital investments.

For reference, here's also how Fama and French themselves describe the CMA factor:

"CMA (Conservative Minus Aggressive) is the average return on the two conservative investment portfolios minus the average return on the two aggressive investment portfolios."

- Fama and French (source)

Limitations to the Fama and French Five Factor Model

Again, like the FFTFM (although to a much lesser degree), the FFFFM is susceptible to misrepresenting the alpha in a regression output, due to the possibility of other factors influencing this alpha. Additionally, the application on thin trading also applies to this model as well.

Fama and French's inclusion and testing on the profitability and investment factors suggested that companies that are small, profitable, value-focused, and have no significant growth factors will generate the highest expected market returns. Additionally, the FFFFM conclusion from the founder's states that the HML factor becomes redundant as the other factors (particularly the CMA, with a 0.7 correlation) already completely describe average returns for a particular security or fund.

Most importantly, this model is limited in its application with small firms that invest greatly despite their typical low amounts of profitability (i.e., positive SMB, negative RMW and CMA). This was proven given the fact that alpha should be statistically indistinguishable from zero, which this all-encompassing model that fully explains stock returns failed to do. There has also been notable research from the U.K. which has suggested the model doesn't work in the U.K. and the model is flawed in terms of how the founders measured profitability.

Regardless, although the FFFFM has its clear limitations and is not yet a proven universal model, the five-factor model still explains between 71-94% of the cross-section variance of expected returns. Additionally, given the model's ability to better explain stock returns with the addition of the RMW and CMA factors, it can still be considered an improvement to the FFTFM.

How to Calculate and Interpret Multifactor Models on Excel

In the rest of this article, I will show you how to interpret and calculate the Fama and French Three Factor, the Carhart Four Factor, and the Fama and French Five Factor models on Excel using regression analysis. This will be a step-by-step instruction. To assist in this instruction, I've provided a completed Excel sheet model below:

In short, to calculate any multifactor model on Excel, you regress the firm's risk-free adjusted returns onto the returns associated with the factors of the particular model. Then, you'd simply interpret the model outputs. Typically, investors are seeking alpha so they would assess whether there's any alpha, what's potentially driving the alpha (e.g., one or more of the risk factors), and whether the alpha is even statistically significant.

Note that when running a regression, you can specify your dependent variable to be the return on your firm minus the risk-free rate. However, this means the risk-free rate is also considered your dependent variable, which raises the assumption that other factors in the multifactor model you're evaluating should be influencing the risk-free rate. Although this could lead to some concern from some investors, it typically does not make a difference in what your results end up being.

How to Interpret Regression Model Outputs

Before running multifactor models regressions on Excel, it's important that you understand what these regression model outputs mean and how to interpret them.

The most important Excel regression ouputs are described below:

• P-Value: In statistics, a p-value less than 5% is considered to be statistically significant (for the null hypothesis to be rejected). In fact, the closer the p-value is to zero, the greater the statistical significance. After running a regression, you'll get a p-value for every regression coefficient. Therefore, if the p-value for alpha or any of the other factors in your multifactor model is greater than 5%, then the computed variable is not statistically significant (not useful).
• Alpha: This is represented by the intercept in a regression output. Alpha measures the overperformance or underperformance of your selected firm or fund. To elaborate, alpha represents the proportion of your selected firm or fund's performance that cannot be attributed to any of the multifactor model factors, or to random miscellaneous movements in the stock market. Clearly, alpha is seen as something investors seek to obtain, although it's important to consider that it can sometimes be misleading as it's sensitive to the model you're using.
• Beta: Beta represents the regression coefficients. These coefficients represent how sensitive and responsive the firm or fund is to the returns on the multifactor model's factors. Put differently, the coefficient tells us the correlation between our dependent variable and the change in that particular regressor (e.g., between expected market return performance and your selected company's performance).
• Residuals: The residuals can be calculated by taking the difference between the firm or fund's actual returns and the returns predicted by the particular multifactor model. The residual is then the standard deviation from this predicted return. In your regression, the average residual should be zero. However, you can take the standard deviation of these residuals, or even the variance of these residuals (standard deviation is just the square root of variance), to evaluate yield idiosyncratic volatility. Again, this explains how much of your firm or fund's returns are attributable to random miscellaneous movements in the stock market.
• R Square: This tells you the explanatory power of the model. The closer this value is to 100%, the greater is the ability of the particular multifactor model to explain returns on your selected firm or fund.
• Adjusted R Square: This is just your R square adjusted for however many parameters you have in the multifactor model.

Besides these outputs,the other miscellaneous pieces of information from the regression output are not-as-important to analyze and therefore will not be discussed in this article.

In any case, there are choices investors must make when constructing the factors that they must be cognizant of, with regards to how they may impact the regression's output results. In fact, it may be wise to cross-validate through several different time period adjustments to ensure that your construction choices aren't creating the artificial appearance of alpha.

Fama and French Three Factor Model Regression Analysis

To interpret the Fama and French Three Factor Model (FFTFM), the best approach is to run a regression on Excel. I will continue with the Home Depot example to assess whether the firm has any significant alpha over the last 5-year period, based on the outputs of the FFTFM.

Step #1: Setup, Download, and Organize the Data

The first step in calculating the FFTFM on Excel is to setup, download, and organize the data to perform our calculation and analysis. These steps are provided below:

1. To perform any type of regression analysis, you must install the "Data Analysis" Excel ToolPak add-in program. Follow these steps to install the add-in on Excel: Open Excel --> File --> Options --> Add-ins --> Go --> Analysis ToolPak --> OK. Restart your Excel if the "Data Analysis" button/text doesn't initially show up under the "Data" tab on the Excel ribbon.
2. Navigate to Yahoo Finance or some other data aggregator website for historical stock market financial data.
3. Download the monthly, weekly, or daily adjusted close price data for your selected company. I typically use a 5-year period and prefer using daily adjusted close price data.
4. Sort your adjusted close price data by ascending order (meaning oldest dates come first). At this point, you should have a date column and a closing price data column.
5. Calculate the monthly, weekly, or daily return percentage for your selected company in a separate column. This formula is simply: [(new date's adjusted close price / previous date's adjusted close price) - 1]. Drag/copy this percentage return calculation to the bottom of your data set.
6. Navigate to Kenneth R. French's website and download the CSV file for "Fama/French 3 Factors [Daily]," assuming you're using daily adjusted close price data. Here, you'll find data on the daily risk-free rate (using the one month T-bill rate instead of the 10-year Treasury rate), the excess market return, the SMB factor, and the HML factor. Divide all of these numbers by 100 to put these values in actual decimal format.
7. Copy the relevant 5-year data over to your originals spreadsheet file and match the dates accordingly. Note that the dates on Fama and French's CSV are shown as "20220630" (Y/M/D). You can change this to the Y/M/D format on Excel via the data split option.
8. Lastly, create a new column to calculate your selected company's excess return percentage. This is just equal to your selected company's return percentage minus the risk-free rate. After this, you should have 8 columns in your data set to run the regression analysis.

Step #2: Run a Regression Analysis

The second step is to simply run a regression on the data set you just put together, given that you now have all of the inputs required to calculate the FFTFM.

1. Assuming you have the "Data Analysis" Excel ToolPak installed, navigate to Data --> Data Analysis --> Regression --> OK.
2. "Input Y Range" is the dependent variable. This will be the excess returns column for your selected company.
3. "Input X Range" is the independent variable. This will be the three risk factors in the Fama and French Three Factor Model (excess market returns, SMB, HML). Therefore, select these three columns and the same exact date range as the dependent variable.
4. Select "Labels" if your column selections has labels in them and select "Regression" if you want to assess idiosyncratic volatility. Choose an output location for your regression and click on the "OK" button.

After this regression is completed, a summary output similar to the one shown below should result (without the formatting):

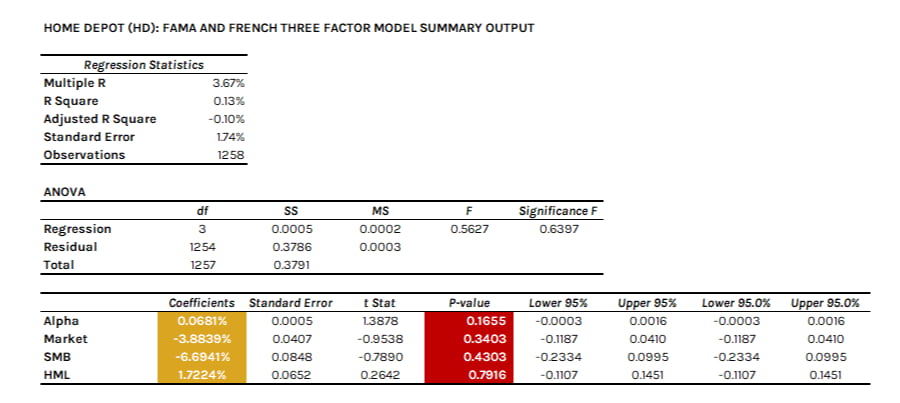
As you can see, because the p-values for alpha and the three risk factors are greater than 5%, the coefficient values are not statistically significant from zero. In specific, the negative SMB factor of -3.9% tells us that Home Depot is not responsive to the SMB factor and is moving in a slightly opposite direction to the returns of small stocks. Therefore, Home Depot is sensitive to how the broader market (particularly larger firms) are performing, which makes sense given it's a large-cap stock.

The HML factor of 1.72% tells us that Home Depot is responsive to the value factor on HML stocks. This also makes sense given that Home Depot has a strong balance sheet and is not really considered a growth stock. Regardless, all inputs are not statistically significant, so the model is of little value.

Note that you can also calculate the Fama and French Three Factor Model on Excel with a formula-based approach:

• For MKT: =INDEX(LINEST(EXCESSMONTHLYRETURN_COLUMN, THREE RISK FACTOR COLUMNS,,1),1,3)
• For SMB: =INDEX(LINEST(EXCESSMONTHLYRETURN_COLUMN, THREE RISK FACTOR COLUMNS,,1),1,2)
• For HML: =INDEX(LINEST(EXCESSMONTHLYRETURN_COLUMN, THREE RISK FACTOR COLUMNS,,1),1,1)

This will give you the same coefficient values for the MKT, SMB, and HML factors in your regression output. You should then calculate the average for each of these columns, in addition to the risk-free rate column. Afterwards, you'd solve for the FFTFM using its formula. Adding one to this result and taking it to the exponent of 252 trading days (assuming you're using daily adjusted close price data) will give you the annual cost of equity for your selected company.

Step #3: Assess Idiosyncratic Volatility

The residuals output describes the random performance occurring on any given day. If you wanted to evaluate idiosyncratic volatility, which is really just the volatility of the residuals, you can accomplish this through this residual output. These steps are shown below:

1. Calculate the variance of the residuals using the =VAR.P Excel formula. Reference the entire residuals column when doing so.
2. Standard deviation is just equal the square root of the variance. Use the =SQRT function on the variance number you just calculated. With our example, we get a standard deviation of 1.7347%, which appears to be relatively small. However, we should keep in mind that the average residual value should be zero, which the next step validates.
3. Use the =AVERAGE function in Excel on the residuals column. Again, this should be equal to zero. Given that the average value for all of your residuals is practically zero, your residuals are outputted in an appropriate manner.

What's important here is to evaluate idiosyncratic volatility (based on the standard deviation output). You should look at how this number compares to other firms over the same exact date range, and rank the company's value accordingly.

Now, as you might've guessed, running and analyzing a regression on the Carhart Four Factor Model (CFFM) and the Fama and French Five Factor Model (FFFFM) follows the same general process. This will be described in the sections below, continuing with our Home Depot example.

Carhart Four Factor Model Regression Analysis

To calculate the CFFM on Excel, repeat everything under step #1 above if not already completed. Then, follow the similar steps below to run this regression:

1. Navigate to Kenneth R. French's website and download the CSV file for "Momentum Factor (Mom) [Daily]," assuming you're using daily adjusted close price data. Here, you'll find data on the daily momentum factor values. Divide all of these numbers by 100 to put these values in actual decimal format.
2. Copy and match these values to the spreadsheet you previously made for the Three Factor Model (replacing you should now have 9 columns in your data set).
3. Now, instead of running the regression on just the three factors, run the regression on all four factors (e.g., dependent variable as excess returns and independent variable as MKT, SMB, HML, and MOM).

As you can see from the regression output above, the momentum factor is also not statistically significant and therefore does not have any explanatory power for Home Depot.

Fama and French Five Factor Model Regression Analysis

1. Navigate to Kenneth R. French's website and download the CSV file for "Fama/French 5 Factors (2x3) [Daily]," assuming you're using daily adjusted close price data. Here, you'll find data on the daily momentum factor values. Divide all of these numbers by 100 to put these values in actual decimal format.
2. Copy and match these values to the spreadsheet you previously made for the Three Factor Model (you should now have 10 columns in your data set).
3. Now, instead of running the regression on just the three factors, run the regression on all five factors (e.g., dependent variable as excess returns and independent variable as excess market return, SMB, HML, RMW, and CMA).

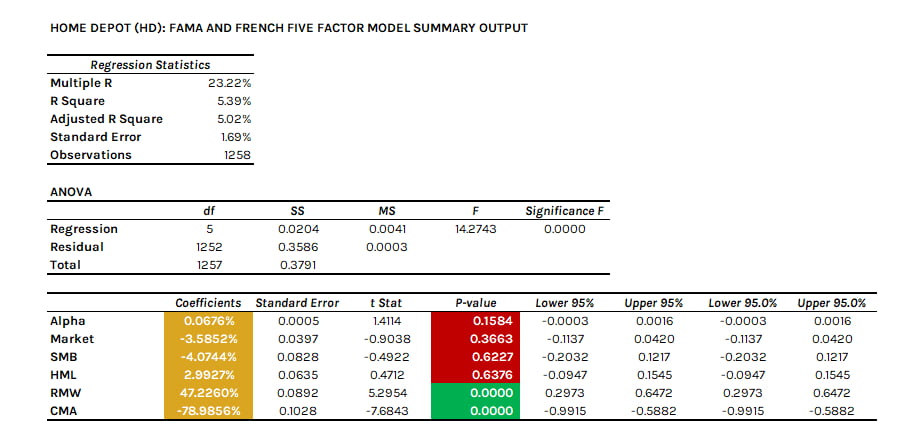
Finally, with the Fama and French Five Factor Model, we have two factors that are statistically significant, given the p-values below 5%. The first, is profitability (RMW), which states that stocks with a high operating profitability perform better than low operating profitability firms. Clearly, Home Depot's positive 47.23% means that its returns are very sensitive to its ability to generate more profit than other smaller firms. This is logical, given the firm's long-term operational profitability.

The second statistically significant factor is the investment (CMA) factor, at a negative -73.99%. This means that Home Depot requires large on-going capital investments to continue growing its business, as opposed to little ongoing capital investment to grow its business.

The Bottom Line

Multifactor models were proposed to argue that additional risk factors, besides just a firm's beta, have a greater explanatory power in driving stock market returns. Through expanding on the Capital Asset Pricing Model (CAPM), which proposes beta is its only risk factor and driver of stock market returns, these multifactor models have been able to improve the understanding on what contributes to stock market returns.

To calculate and interpret the Fama and French and Carhart multifactor models, the best approach is to run a regression analysis on Excel and then to interpret the model's outputs. In our example, we used a specific company's returns, but this can be replaced for any publicly tradable security or fund, so long as it has enough historical market data to analyze. In fact, it's more logical to use a fund or your own stock portfolio for regression analysis, given that you're trying to seek and assess alpha.

In short, this process is to get the selected firm or fund's stock market returns, subtract them by the risk-free rate, and then line these excess returns appropriately with the risk factors from Kenneth French's website (by date). Afterwards, you can run a regression on Excel using the Data Analysis ToolPak, with the excess returns as the dependent variable and the risk factors as the independent variables. Investors should then assess the statistical significance of alpha and beta coefficients to understand the explanatory power of the model and the potential performance expected from investing in the particular security or fund.

Given that the four- and five factor models explain up to 95% of portfolio stock market returns, there's a limited practical benefit in continuing to include additional factors (e.g., by including popular factors not included in these models such as the low-volatility and quality factors). Furthermore, given that these mathematical frameworks for the multifactor models are already established, easily comparable between portfolios, and even somewhat redundant, there's little upside potential in including additional factors in an attempt to further explain the returns of a particular stock.