In this article, I will show you how to apply comparable company analysis using valuation multiples, and will use this valuation method to value a real company in the stock market. Comparable company analysis (aka relative valuation or valuation using multiples) is the most popular valuation practice, where you're comparing a company to its peers and implying its worth based on appropriate relative trading multiples. This is based on the premise that similar companies share key business and financial characteristics, performance drivers, and risks.

Analysts and investors can therefore determine a company's relative position among peer companies, primarily based on the current value from market condition, and can determine a valuation. Like all valuation methods, relative valuation does come with its advantages and disadvantages as well, so we'll also discuss best uses for relative valuation and how viable and effective the method is when valuing companies in the stock market.

Relative Valuation Explained

Relative valuation is dependent on how similar assets are priced in the market. The objective with relative valuation is therefore to value an asset based on how similar assets are currently priced in the market. This is different from absolute valuation methods such as the discounted cash flow (DCF) calculation, as this entails estimating the intrinsic/fair value of a company based on its cash flows and growth potential without comparing it to other similar assets whatsoever.

To better illustrate the principle of relative valuation, we can look at how property is valued within the real estate market. To begin, a property on its own represents a productive cash generating asset, which implies the property has an intrinsic value. However, in most cases, to understand the real price of a property, you must compare its price to other nearby similar properties that have recently sold. For example, if an identical similarly-sized house sold across the street recently for $500,000, it's unlikely that you'll be able to buy an identical house now for half the price ($250,000).

In the same way, companies in the stock market all have an intrinsic value that can be more or less estimated, and most are similar-enough to other companies within their industry. Therefore, the concept of relative valuation can be applied to companies as well.

Because relative valuation is based on the value of similar assets, you must evaluate a company relative to its peers, such as those within the same industry/sector and those with a similar business model. Typically, these peers would be considered direct competitors, such as those operating in the same or in a closely-related industry/sector, and/or companies with the same size, quality, and even growth attributes. Ultimately, this decision on selecting the appropriate peers will be based on your knowledge of a particular company and its respective industry/sector.

Now that we understand the concept of relative valuation, we can look at the general steps to completing a relative valuation. These five steps, as shown in the table of contents, are listed below as well:

• Step 1: Determine an Appropriate Set of Company Comparables
• Step 2: Aggregate and Standardize Financial Data
• Step 3: Select Appropriate Trading Multiples, Key Statistics, and Ratios
• Step 4: Benchmark the Comparable Companies
• Step 5: Imply Valuation

In this article, we will complete a comparable company analysis using valuation multiples for Cedar Fair (FUN), a company that operates amusement park-resorts throughout the U.S. and Canada.

You can see Cedar Fair's stock price performance over time in the chart below:

Step #1: Determine an Appropriate Set of Company Comparables

The first step is to determine an appropriate set of company comparables (aka comps). This is the foundation of a relative valuation approach. Although this can be fairly simple and intuitive for companies in certain sectors, it can also be quite challenging for other companies and/or industries where peers are not as obvious.

Therefore, before you even begin a relative valuation approach, you must understand the company you're trying to value (the target company) thoroughly. Put simply, this entails considering the target company's business and financial profile. I would begin by evaluating the target company's business profile first, as the financial profile measures typically confirm what you previously found.

Note: This list is based on Investment Banking: Valuation, Leveraged Buyouts, and Mergers and Acquisitions (2013).

Clearly, you need to select the right companies to compare the target company to. It's in your best interest to not rush through this due diligence process and make assumptions, otherwise your valuation model can be very misleading. Ultimately, the more you read and study about a company, its sector, and its business operations, the more accurate your model may end up being.

As previously mentioned, the methodology for determining comps is relatively intuitive, and typically involves looking at companies within the same sector (or sub-sector) and those with similar sizes. However, this can be quite challenging for certain companies and industries where peers are not as obvious. Regardless, the actual selection of comps should not begin until you've thoroughly understood the target company.

Companies With No Comps

For companies with no clear comps, one can examine companies outside the target company's industry/sector and select companies that share similar business and financial characteristics. For further analysis, The multiple of a specific company can also be compared to the average of that industry/sector, instead of select comps. Additionally, multiples can also be compared to the company's long-term historical averages to determine how undervalued or overvalued the current multiple is trading at.

For example, the graph above shows that Cedar Fair's current price-to-sales (P/S) ratio is very overvalued, relative to the previous 15 years, due the effects of the pandemic (slower sales) and the company's current stock trading price. You could do the same with other ratios, key statistics, and multiples discussed later in this article, and then apply the ones most relevant to the target company's business model and industry/sector.

Where to Find Comps

The initial screening stage focus is on identifying companies with a similar business profile. In your business and financial profile valuation process, you may have uncovered potential comps. The target company may also discuss its competitors to shareholders during earnings calls or in their 10-K annual reports, particularly in the "management's discussion and analysis" section. Besides this, you can use various financial services websites or a simple Google search to uncover additional comps.

The websites I use include:

• Yahoo Finance: Search for a company and look under "People Also Watch" on the right sidebar.
• MarketBeat: Search for a company and look under the "Competitors" tab.
• Morningstar: Search for a company and look under the "Stock Analysis" tab

Cedar Fair Comps

Cedar Fair's comps can be determined rather quickly given its business model, which revolves around operating its amusement parks, water parks, and resort facilities in the U.S. and Canada.. For context on where Cedar Fair fits in the industry, they're the world's 8th largest amusement park by attendance (4th largest in the U.S.). The largest competitors include Walt Disney Parks & Resorts, Six Flags Entertainment, and SeaWorld Parks & Entertainment, which are the "pure play" competitors to Cedar Fair.

We can also look at Cedar Fair's revenue breakdown, to better understand the company's operations and what peers we should be looking for. This is broken down in the pie charts below from 2018-2020:

As you can see, Cedar Fair drives much of its revenue from amusement park admissions, which are simply just the admission fees customer's pay to access the parks, including parking fees. Food, merchandise and games that the park offers both inside and outside the park are also significant revenue drivers. However, only about 15% of its revenue comes from "accommodations and other," which includes "extra-charge products, including premium benefit offerings such as front-of-line products and online transaction fees charged to customers," per Cedar Fair's most recent 10-K annual report.

Based on Cedar Fair's business model, revenue breakdown, its scale, and where it operates, among other business and financial profile measures, the list of competitors I will use for this relative valuation model are listed below:

• Six Flags Entertainment Corporation (SIX): Operates regional theme and water parks across the U.S., Mexico, and Canada.
• SeaWorld Entertainment (SEAS): Operates as a theme park and entertainment company across the U.S.
• The Walt Disney Company (DIS): A worldwide entertainment company. Only about 22% of its revenue comes from its operations of theme parks and resorts, so this is something to keep in mind.
• Vail Resorts (MTN): Operates mountain resorts and urban ski areas in the U.S. Revenues are generated from mountain and lodging services along with retail and dining, much like amusement parks.

I'll also be taking a closer look into the top two publicly traded movie theater companies in the U.S. (by market capitalization), as they're entertainment-focused that also happen to generate much of their revenue from ticket sales (admissions) and food/beverage, like Cedar Fair, while also being impacted heavily by the pandemic like amusement parks have been. Lastly, I'll consider Marcus Corporation, whose business model is not entirely dependent or directly related to amusement park resorts or theaters.

• AMC Entertainment Holdings (AMC): Provides movie theater services and operates in the U.S. and in Europe.
• Cinemark Holdings (CNK): Owns and operates movie theaters throughout the U.S. and in 12 Latin American countries.
• Marcus Corporation (MCS): Engaged in the Theaters and Hotels and Resorts business segments across the U.S.

After identifying these similar companies (comps), the next step is to find financial data, and then aggregate and standardize the data so that it can be compared.

Step #2: Aggregate and Standardize Financial Data

Once the initial comps are determined, you must locate the financial data needed to analyze the selected comps and calculate trading multiples, key financial statistics, and ratios (in step #3). To aggregate and standardize data, you can use the most recent 10-K, 10-Q, 8-K, or Press Release information to find the necessary financial information. The Proxy Statement and credit rating agencies may also help in providing relevant information.

Once you have the necessary financial information for all of the comps, you should create an "input page," where the calculation of the key financial statistics, ratios, and multiples can be completed. This will then feed into the output sheets that are then used to benchmark the comps. However, because these multiples are already calculated for us in our example (shown later below), this process is not required.

Using a financial data website can speed up this process quite significantly. Below are four free websites I like to use for relative valuation (some may require registration):

• Yahoo Finance: Search for a company and look under "Statistics," then under "Valuation Measures."
• TIKR: Search for a company and click on the "Valuation" tab. Look under "Multiples."
• Atom Finance: Go to "Hubs," click on "Search Tickers," type in the stock tickers for your company and its competitors you identified in Step #1. Then, click on "Save as hub." You can choose to export this data as "default columns" and as "returns."
• QuickFS: Search for a company and look at the "Key Statistics" table.

If I were using Atom Finance, as I did in this article, I would download the two Excel sheets ('default columns,' which has multiples data and 'returns,' which has various performance information) and then put them on one spreadsheet. Then, I would clean this data so that the formatting is consistent throughout (i.e., ensure all data is in number format). Afterwards, I would copy relevant data from each sheet into one sheet, and then identify which multiples are the most relevant depending on the company and the industry it's in, which the next step covers.

Step #3: Select Appropriate Trading Multiples, Key Statistics, and Ratios

Because companies can have dramatically different sizes, revenues, and bottom-line earnings, investors can use trading multiples, ratios, and other KPIs to make comparing two or more different assets a lot easier. Multiples are therefore used in relative valuation to give investors an idea on how "expensive" a company is, relative to its peers.

The logic with valuation multiples, is that the company you're trying to value should have similar earnings to its competitors, given that it's operating within the same industry/sector and possesses similar characteristics. The default approach to valuation multiples is rather straightforward, in which a table (or multiple tables) are organized so that different valuation multiples from similar companies can be compared to one another. In theory, these ratios should help you to identify how cheap or expensive a business is.

In general, valuation multiples can be thought of the ratio between the valuation of a company and a particular trading metric:

Valuation multiple = Value of a company / Financial or business metric

Most valuation metrics therefore follow the same approach, where the company's stock price, market cap, or enterprise value are evaluated in respect to some other metric, such as a firm's profit or cash flow.

Below are the key financial statistics that are standard in the relative valuation approach:

• Market Valuation (Size): Equity value and enterprise value.
• Profitability: EBITDA, EBIT, gross profit, and net income margins.
• Growth Profile: Historical and estimated growth rates.
• Return on Investment (ROI): Return on invested capital (ROIC), return on equity (ROE), return on assets (ROA), and dividend yield.
• Credit Profile: Leverage ratios, coverage ratios, and credit ratings.

These key financial statistics are described in detail below.

Equity Value

Equity value represents a company's fully diluted shares outstanding (different from basic shares outstanding) multiplied by the current share price. In comparison to other companies, this measure is only useful for understanding the relative size of a company.

Equity value = Share price * Fully diluted shares outstanding

where:

Fully diluted shares outstanding = Basic shares outstanding + "In-the-money" options and warrants + "In-the-money" convertible securities

Basic shares outstanding can easily be found from the first page of a company's 10-K or 10-Q. Otherwise, it is usually reported on most financial data websites as well. "In-the-money" options and warrants can be calculated using the "treasury stock method"(TSM). "In-the-money" convertible securities can be calculated with the "if-converted method."

The easier method, however, is to just look at the income statement in the most recent 10-K or 10-Q report, and look towards the bottom of the income statement where a line item called "Shares used in computing earnings per share (EPS)," or something similar should be stated. Then, a sub-section should show Basic and Diluted shares outstanding, and you can use this Diluted figure to calculate equity value. The accompanying "notes to consolidated financial statements," found under the financial statements, will typically provide you with more detail on this calculation as well.

This is outlined below from Cedar Fair's most recent (FY 2020) 10-K annual report, on its income statement:

If you know the enterprise value, you can calculate equity value as well (without having to worry about diluted shares outstanding):

Equity value = Enterprise value - Debt and debt equivalents - Non-controlling interest - Preferred stock + Cash and cash equivalents

Note that debt and debt equivalents, non-controlling interest (aka minority interest), and preferred stock are subtracted because they represent the share of other shareholders.

% of 52-Week High

For insight on the absolute and relative market performance, investors can look at the company's current share price as a percentage (%) of its 52-week high. This metric gives investors perspective on valuation, on the current market sentiment, and on the overall outlook for the broader industry/sector. Comparing the target company and the comps "% of 52-week high" will provide insight on whether the target company is aligned with its peers from a performance and current market value perspective, or if there are individual things that may be affecting the company's performance.

Ideally, your comps should be within a 5% deviation range from your target company's % of 52-week high figure. For example, if the average of five comps is 50%, and the % of 52-week high is between 45% and 55%, then they're likely very similar (from a market performance perspective and business/financial profile perspective), which is what we're looking for in comps.

You can calculate the % of 52-week high using the formula below, which is rather intuitive:

% of 52-week high = Share price / 52-week high

This will be calculated and examined in our Cedar Fair example as well.

Enterprise Value

Enterprise value is the sum of all ownership interest in a company and claims on its assets from both debt and equity holders. Changes in a company's capital structure will not affect its enterprise value, which is why enterprise value multiples are used more frequently than equity value multiples. Therefore, by using the enterprise value, you're conducting an unbiased comparison for different companies that likely have different capital structures. Ultimately, this can help in setting up a more "fair" environment to compare companies. On the other hand, with equity value multiples, the capital structure of comps can influence the resulting equity value.

The enterprise value calculation is shown below:

Enterprise value = Equity value + Total debt + Preferred Stock + Non-controlling interest - Cash and cash equivalents

where:

• Equity value = share price * fully diluted shares outstanding
• Total debt = short-term debt + long-term debt

To determine whether or not a company has preferred stock outstanding, you can look under the shareholders' equity section of a company's balance sheet. Note that many companies do not issue preferred stock. In this case, the preferred stock figure would just be zero (nonexistent).

Non-controlling interest is also called "minority interest." This can be found in the balance sheet, under the non-current liability section or equity section. This will only show up if the company owns more than 50% of another company (the subsidiary), in terms of the subsidiaries voting stock.

Cash and cash equivalents can simply be found under the "current assets" section on the balance sheet, which are the most liquid assets a company has. "Cash equivalents" refer to to short-term commitments that are likely accruing interest, like money market funds, that can be easily converted into a known cash amount.

Profitability Metrics

Below is a list of common multiple profitability metrics you can calculate/use in your relative valuation approach, along with a more detailed description of EBTIDA and EBIT:

EBITDA

EBITDA (Earnings Before Interest, Taxes, Depreciation, and Amortization), is a widely used measure for operating cash flow and profitability, as it reflects the company's total cash operating costs for producing its products, ignoring financing costs and non-cash charges. EBITDA is free of differences that result from tax regime (e.g, tax expense) and capital structure (e.g., interest expense), which makes the figure ideal for an "apples-to-apples" comparison between comps.

EBIT

EBIT (Earnings Before Interest and Taxes) is independent of tax regime and serves as a useful metric for comparing companies with different capital structures. It's often synonymous with "operating income," "operating profit," or "income from operations," found on the income statement. Because EBIT includes non-cash depreciation and amortization (D&A) expense, it's less indicative as a measure of operating cash flow.

Leverage Metrics

Below is a list of common multiple leverage metrics you can calculate/use in your relative valuation approach:

Calendarization of Financial Data

Many publicly-traded companies in the U.S. report their financial performance in accordance with a fiscal year (FY) ending on December 31st. This corresponds to the calendar year (CY) end. However, not all companies report their FY end on December 31st, so for comps benchmarking purposes, any variation in fiscal year end's among comps must be addressed.

You can use the formula below to "calendarize" the financial data for whatever metric you're using. In this case, I'll use sales as an example:

Next calendar year (CY) sales = [(Month #) * (FYA sales) / 12] + [(12 - Month #) * (NFY sales) / 12]

where:

• Month # = the month in which the company's fiscal year (FY) ends (e.g., "3" for FY ending March 31st)
• FYA = fiscal year actual
• NFY = next fiscal year

If needed, this is important to do, as trading multiples based on financial data for different periods can lead to a misleading comps valuation, especially for cyclical companies and industries.

Equity Value Multiples

Three common equity value multiples are the price-to-earnings (P/E) ratio, the price/earnings-to-growth (PEG) ratio, and the equity value to net income (EV/NI) multiple.

P/E Ratio

P/E ratios provide a measure on how much investors are willing to pay for a dollar of a company's current or future earnings. Typically, P/E ratios are typically based on forward-year earnings-per-share (EPS) figures, as investors are focused on future growth. Companies with higher P/E ratios than their peers tend to have higher earnings growth expectations.

P/E ratio = Share price / Earnings per share (EPS)

The earnings per share (EPS) number can be found using the formula below:

Earnings per share (EPS) = (Net income - Preferred dividends) / Weighted average of common shares outstanding

P/E ratios (and other multiples) also offer several ways to look at the same multiple. Different method of examining the P/E ratio are shown below:

• Classic P/E: Based on the last fiscal year. This is a 12-month period that companies use for accounting purposesnn . For example, one company's fiscal year (FY) may end in October while others may end in December.
• Trailing P/E: Based on the last four quarters added together. Trailing 12 months (TTM or LTM) is the term used for the data from the past 12 consecutive months for reporting financial figures.
• Forward P/E: This ratio divides the current price of the stock by the estimated future earnings per share, for example based on what analysts believe. Although this can be insightful, approach forecast metrics with caution as they're obviously predicting the uncertain future and are using growth rates separate from ones you may have for the company.

In general, a lower P/E ratio is "better" as it means that you get more earnings from your investment. However, this can also mean that investors aren't very confident about the company's current standing. On the other hand, a higher P/E ratio means investors are paying a higher price for the stock when compared to its earnings. In addition, as the P/E ratio increases, it shows that the current investor sentiment is favorable, meaning investors are willing to pay a higher price for the stock. By contrast, a declining P/E is an indication that the sentiment is turning bearish.

PEG Ratio

Compared to other ratios, the PEG ratio is unique as it factors in growth, and is generally a more valuable multiple than the P/E ratio itself. In other words, because the PEG ratio factors in expected levels of growth across different comps, it's a better multiple to compare with its peers, even if they are in different business life cycles. This ratio can also be divided up into the trailing PEG for historical growth rates, and the forward PEG for forward-looking growth rates.

PEG ratio = P/E ratio / Earnings per share (EPS) growth rate

The PEG ratio can therefore be used instead of the forward-looking P/E ratio, as it generally provides a more complete picture of a company's value. If the PEG ratio is below 1.0, it's indicative of an undervalued stock because you'd be receiving more growth than you're paying for. The opposite would apply for a PEG ratio above 1.0.

EV/NI Multiple

The EV/NI multiple is a ratio that illustrates how much an investor is willing to pay for a dollar of a company's current or future earnings. This is the better equity value multiple to use in many cases, as the P/E and PEG ratios ignore balance sheet strength and capital structure.

EV/NI = Equity value (EV) / Net income (NI)

where:

• Equity value (EV) = Share price * Fully diluted shares outstanding

The two limits to the EV/NI multiple are listed below:

1. Because EV/NI includes net income, financing costs and the capital structure of a company impacts the denominator. Therefore, comparing companies with different capital structures is unfair (as previously discussed).
2. If the company has low or zero earnings (no net profit/income), the measure is not useful for analysis.

Enterprise Value Multiples

Because enterprise value represents the interests of both debt and equity holders, it's used as a multiple for key financial statistics such as sales, EBITDA, and EBIT. Enterprise value multiples are therefore more appropriate when trying to value an entire business.

The most common enterprise value multiples are "enterprise-value-to-EBITDA" (EV/EBITDA) and "enterprise-value-to-EBIT" (EV/EBIT). These are the general valuation standards for most sectors, and they also act independently of capital structure, taxes, and depreciation and amortization differences among different companies.

Enterprise Value to Free Cash Flow (EV/FCF)

EV/FCF compares the enterprise value to the company's ability to generate cash flow. The lower this ratio, the quicker a company can generate cash to reinvest in its business or payout to shareholders in the form of dividends.

Enterprise Value-to-Sales Multiple (EV/S)

EV/S compares the enterprise value to the company's ability to generate sales. However, sales (revenue), although it does provide an indication of size, does not translate well into profitability or cash flow generation, which is why it's typically less relevant than other enterprise value multiples.

Sector-Specific Multiples

Sector-specific multiples can be applied to certain industries/sectors if they are more relevant. These multiples use an indicator of market valuation (e.g., equity value or enterprise value) in the numerator and key sector-specific production/capacity, financial, or operational statistic in the denominator.

These sector-specific multiples can be divided up into "items affected by capital structure" (equity value (price) in the numerator) and "items unaffected by capital structure" (enterprise value in the numerator).

Items affected by capital structure:

Items unaffected by capital structure:

Cedar Fair Multiples

For Cedar Fair, to keep things simple, and because I'm interested in how it will perform in the future with the entertainment industry's current slump due to the pandemic, I'm going to be focusing on forward multiples. This means that I will get rid of any "LTM" or "TTM" (last/trailing twelve months) data that I received from Atom Finance. I'm also going to ignore EPS Growth (FY1), because many of these comparable companies, Cedar Fair included, did not generate much of a profit over the last year.

Step #4: Benchmark the Comparable Companies

The next part of the analysis process is to examine the comparable companies (aka comps) and determine the target company's relative ranking and closest competitors. Again, the target company is simply the company you're trying to value. Benchmarking therefore serves to determine the relative strength of the comparable companies in relation to one another and the target company. This entails closely examining the similarities and discrepancies in size, margins, and growth rates, among other measures, between the comps and the target company. Ultimately, the objective is to determine the target company's relative ranking so that valuation can be framed accordingly.

The two steps for this process are as follows:

1. Benchmark the Financial Statistics and Ratios: This refers to measures of size, profitability, growth, returns, and credit strength, among other key financial statistics and ratios to determine the independent strength of the comps.
2. Benchmark the Trading Multiples: This refers to the EV/EBITDA, EV/EBIT, and other enterprise and equity value multiples you're comparing.

When benchmarking, you'll need to calculate the medians and means (averages) to get a better sense of where the comps are trading at. You should do this for each category and for the overall total as well. Additionally, you should title every column appropriately and organize them accordingly, as I did here for Cedar Fair:

Shown above is the standard format to use for a comparable companies analysis. It appears that Six Flags and SeaWorld are poised for higher growth than the other two comps in the "Amusement Park/Resorts" category, which makes sense given the reopening of amusement parks/resorts throughout the U.S. and other countries.

We can now use this benchmarked information to imply a valuation for Cedar Fair.

Step #5: Imply Valuation

The final step utilizes the trading multiples of the comparable companies to derive a valuation range for the target company. This entails calculating and using the means (averages) and medians for the appropriate trading multiples (e.g., EV/EBITDA) as the basis for extrapolating an initial range, as previously illustrated. The high and low (outlier) multiples for the comps serve as further guidance in terms of a potential ceiling or floor for the valuation.

Valuation Implied by EV/EBITDA

For our Cedar Fair example, now that everything is bencharked, multiples can be applied for valuation purposes. We'll be using EV/EBITDA to imply a valuation for Cedar Fair. I used Yahoo Finance analyst estimates for Cedar Fair's revenue in 2021 and 2022. Then, I used Atom Finance and TIKR to provide me an estimate on EBITDA for 2021 and 2022. You can also use net income as a proxy for EBITDA, if you're unable to find an accurate estimate for EBITDA, or just estimate one yourself based on your understanding of the company or the company's historical EBITDA growth rates.

These estimated financials for Cedar Fair are shown below:

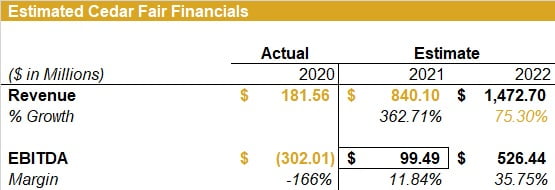
Looking back at the comps table/image in the previous section, I decided to use the "Amusement Parks/Resorts" average EBITDA FY1 multiple of 31.28x, because it's slightly more conservative. If I wanted a valuation range, then I could've used the 32.15x as well. Then, I used the EBITDA estimate for 2021 ($99.49 million), as it was more realistic, to make on estimate on the valuation of Cedar Fair. Finally, I divided by the fully diluted shares outstanding (shown before) to get the implied share price.

These steps are also shown below:

• Step 1: 31.28x EV/EBITDA * $99.49 million EBITDA = $3,112.0472
• Step 2: $3,112.0472 / 56.746 million diluted shares outstanding = $55.10 (implied share price)

Comparing this to the share price on 04/23/2021 of $50.12, we can imply that Cedar Fair's current share trading price is undervalued on a purely relative basis (by 9.94%).

Best Uses and Limitations for Relative Valuation

While relative valuation is rather intuitive, it does come with its advantages and disadvantages (like all other valuation methods). The two sub-section below should therefore give you an understanding on how viable the method is, depending on the target company and respective industry, and when it may provide the most use to the average retail investor.

Pros of Relative Valuation

• Market-Based: Valuation is derived from actual market data. This helps to reflect the market's growth and risk expectations, along with making the valuation comparable and easily measurable when compared to comps.
• Simple and Convenient: Relative valuation can be quicker than a DCF calculation, as it can be determined on the basis of a few simple calculated inputs. These calculations typically involve simple arithmetic operations, which is only sped-up with the help of financial data websites.
• Current: Market data multiples are updated on a daily (or intraday) basis, unlike data sourced from a company filing, which favors multiples/ratios that vary depending on the company's stock price.
• Ignores Free Cash Flow: Because relative valuation does not imply the value of a company from its free cash flow (FCF), it's generally a more appropriate valuation method to use over an absolute valuation method, especially for companies with little-to-none in FCF. This can include high-tech growth companies, unprofitable companies, or those with inconsistent FCFs.
• Adaptability: Many different multiples, key statistics, and ratios can be used to value different companies and industries/sectors, making the relative valuation approach very adaptable.

Relative valuation is clearly most appropriate in an "apples-to-apples" comparison, not an "apples-and-oranges" comparison. Theoretically, the more confident an investor is with its comps, the more helpful performance, profitability, and leverage ratios will be in estimating an implied share price. For example, Delta (DAL) and Boeing (BA) have very similar business models and it may be worth comparing the two companies. However, the same could likely not be said for a dine-in restaurant and a fast food chain, even though they are both in the restaurant industry.

Cons of Relative Valuation

• Market-Based: Although relative valuation reflects the market's current growth and risk expectations, when the market is overly-volatile or extremely overvalued/undervalued, these multiples can be skewed.
• Finding Relevant Comps: "Pure play" comps may be difficult to identify if the target company is in a niche segment, which can result in less accurate and valuable comps. Moreover, the relative valuation approach is somewhat artificial, as no two companies are truly alike.
• Ignores Company-Specific Issues and Free Cash Flow: The target company valuation, by nature of relative valuation, is based on other comps. This completely ignores any company-specific strengths or weaknesses of the target company, along with the target company's FCF, which can be used to derive an intrinsic/fair value price for a business.
• Assumption of Stock Worth: Just because a stock is cheap on a relative basis, does not preclude that the stock is cheap in absolute terms. To elaborate, if a stock is trading at all-time high valuation multiples but appears lower than its peers, you obviously would not just buy the stock based on this alone.
• Ignores Industry-Specific Valuation: Industry-specific valuation multiples may be above historical norms, and may not project the future growth prospects of that industry. If two comps are trading at excess levels (e.g., P/E ratios around 100x), and one company happens to have a lower P/E ratio, this does not necessarily mean the company trading at a lower P/E ratio is cheap in absolute terms.
• Vulnerable to Manipulation: Valuation multiple approaches are vulnerable to manipulation. In other words, biased investors/analysts can choose whatever multiple or set of comps they'd like, and can justify any sort of valuation.

With relative valuation, your basis is that the market knows how to price every single business correctly (called the efficient market hypothesis), which is generally proven to be false. Relative valuation also gives no information on what a company's intrinsic worth is, and as a result, the stock may be undervalued on a relative basis but overvalued on an absolute basis (e.g., with a DCF valuation). I therefore believe the relative valuation approach, although useful at times, is inferior to other valuation approaches. In fact, using relative valuation methods may expose you to psychological biases (e.g., anchoring bias), where the target company and its growth trajectory may have changed and therefore the business may deserve to trade at a higher multiple. Clearly, all of this is not reflected in a valuation multiples approach.

The Bottom Line

To value a company using comparable company analysis (aka relative valuation or valuation using multiples), you must begin by identifying an appropriate set of peers (aka comps), which your model will be based on. Afterwards, you need to locate and then aggregate and standardize the appropriate financial data needed for all of the chosen comps. Then, you can select the appropriate trading multiples, key statistics, and ratios depending on the target company and its respective industry/sector. Next, you need to benchmark this information, calculate medians and means, and select a valuation multiple that best suites the target company.

The final step is to imply valuation, for example, based on a median/average multiple such as EV/EBITDA, and determine a valuation by multiplying this number to a future expected EBITDA number. Dividing by the diluted shares outstanding will then provide you with an implied share price that you can then compare to the current trading price. A range of implied share prices can also be determined if you select another appropriate EV/EBITDA median/average multiple and repeat this process.

Although this process is rather intuitive and is often seen as a "shortcut valuation approach" for many companies, relative valuation fails to provide information on the growth prospects of the target company, the quality of management, the competitive position of the corporation, its cash flow generation abilities, and many other company-specific attributes. Nonetheless, relative valuation can be a good starting point for understanding a company's current market position, along with being particularly useful for companies with little-to-none in free cash flow, or unprofitable companies.

As a rule of thumb, in the short-term, valuation multiples are the primary drivers of stock price performance. However, in the long-run, business growth drives stock performance. Business growth is also typically a lot more easier to predict, which is why investors should focus on the business fundamentals and qualities first. In closing, while valuation multiples are popular due to their simplicity, a discounted cash flow (DCF) valuation (based on absolute valuation) may give you an edge in the market, especially for long-term value investors who manage to develop a solid understanding of a particular business and its growth potential.