In this article, I will demonstrate how to use the Two-Stage Dividend Discount Model (DDM) to value dividend-paying stocks. This model is a refined version of the traditional dividend discount approach, incorporating two distinct phases of dividend growth: initially, a phase of irregular or extraordinary growth, followed by a phase of stable growth into perpetuity. This two-phase approach provides a more detailed understanding of a company's growth trajectory and its evolution over time.

This article will detail the model's formula, explore its fundamental assumptions, identify scenarios where it is most effective, discuss its limitations in stock valuation, and conclude with a comprehensive example demonstrating the practical application of the Two-Stage DDM.

Two-Stage Dividend Discount Model Explanation

The Two-Stage Dividend Discount Model (DDM) extends the basic principles of the Gordon Growth Model (GGM). It evaluates the present value of a future series of dividends expected to grow at a consistent rate indefinitely. Unlike the GGM, the Two-Stage Model incorporates a more dynamic view of a company's growth. This is particularly useful for firms experiencing significant shifts in their growth trajectory.

The figure below depicts the expected dividend growth over time in the Two-Stage DDM:

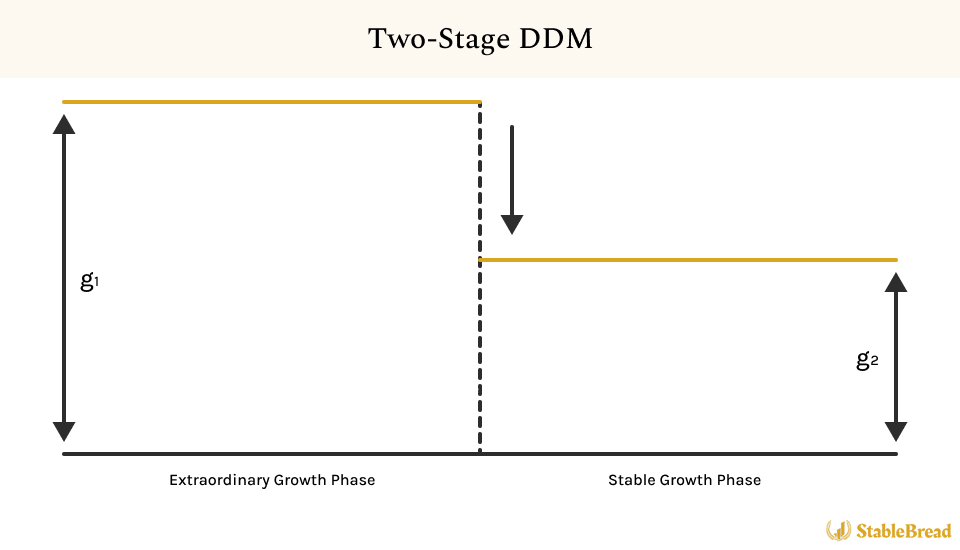
In the Two-Stage DDM, two distinct growth phases are identified. The initial phase, often characterized by an irregular, often higher, growth rate, corresponds to a company's period of rapid expansion or significant market entry. This is followed by a more predictable phase, where the growth rate stabilizes, and dividends are expected to grow at this consistent rate indefinitely. The model excels at calculating the present value of dividends across these different growth stages, offering a detailed view of a company's dividend growth pattern over time.

The model's versatility is noteworthy. While the initial phase usually has a higher growth rate than the stable phase, it can also accommodate scenarios where a company might experience low or even negative growth rates before transitioning to stable growth. This adaptability makes the Two-Stage Model relevant for valuing a wide range of companies, including those in volatile industries or undergoing significant structural changes. Thus, the Two-Stage Model's strength lies in its ability to reflect the complexities of a company's growth journey, especially when this journey is not linear.

Two-Stage Dividend Discount Model Formulas

In this section, two Two-Stage Dividend Discount Model (DDM) formulas are discussed. The sole difference between them lies in how the dividends in the extraordinary growth phase are estimated.

Two-Stage DDM Formula: Option #1

The first Two-Stage DDM formula is shown below:

where:

• P₀ = stock's fair value (at year 0)
• DPS_t = annual dividends per share (in year t)
• n = final year of first-stage dividend growth (i.e., when dividend growth changes from g₁ to g₂)
• g₁ = extraordinary high/low dividend growth rate (first stage)
• g₂ = perpetual dividend growth rate (second stage)
• r_e,1 = first growth period discount rate (aka required rate of return)
• r_e,2 = stable growth period discount rate (aka required rate of return)

The first Two-Stage DDM formula, also known as the "Variable (Non-Constant) Growth Dividend Discount Model," requires estimating dividend growth for each period during the initial n years of the extraordinary growth phase. Present values for these periods are calculated and aggregated to determine the stock's value during this phase. Although this method is slightly more intricate, it may offer a more precise depiction of a stock's intrinsic value, aligning more closely with the actual dividend payment policies of businesses.

Two-Stage DDM Formula: Option #2

Now, if you assume that the extraordinary growth rate (g₁) and the dividend payout ratio (DPR) remain constant for the first n years, then the following simplified Two-Stage DDM formula can be utilized instead:

where:

• P₀ = stock's fair value (at year 0)
• DPS₀ = annual dividends per share (at year 0)
• n = final year of first-stage dividend growth (i.e., when dividend growth changes from g₁ to g₂)
• g₁ = extraordinary high/low dividend growth rate (first stage)
• g₂ = perpetual dividend growth rate (second stage)
• r_e,1 = first growth period discount rate (aka required rate of return)
• r_e,2 = stable growth period discount rate (aka required rate of return)

Unlike option #1, the second Two-Stage DDM formula simplifies the process by eliminating the need to estimate dividends annually for the initial n years of the extraordinary growth phase. It operates under the assumption that dividends in the first stage will continue to grow at the same extraordinary rate, thereby implying a constant dividend payout ratio. Although theoretically less precise than the first Two-Stage DDM formula, this approach is more commonly utilized, primarily because it demands less estimation and is more manageable for most investors, striking a balance between accuracy and practicality. This is also the formula we'll focus on for the purposes of this article.

To understand the simplified Two-Stage DDM formula further, let's deconstruct it into its two constituent phases:

1. First Phase (Extraordinary Growth Phase): In the first phase of the Two-Stage DDM, we calculate the present value of dividends during the initial growth period, using the current dividend (DPS₀) which is projected to grow at an extraordinary rate (g₁) for n years. The term "((1 + g₁)ⁿ / (1 + r_e,1)ⁿ)" computes the present value proportion of the compounded dividend at the end of n years. By subtracting this from 1 and multiplying with DPS₀ adjusted for the first year's growth, we determine the present value of dividends during this extraordinary growth phase. The denominator "(r_e,1 - g₁)" calculates the effective discount rate, reflecting the difference between the discount rate (r_e,1) and the dividend growth rate. The discount rate, often derived from the Capital Asset Pricing Model (CAPM), accounts for the risk-return profile during this phase, linking expected stock returns to market risk.
2. Second Phase (Stable Growth Phase): After the extraordinary growth phase ends at year n, the Two-Stage DDM transitions into a stable growth phase (g₂). In this phase, the discount rate (r_e,2) may differ from the initial phase's rate (r_e,1), reflecting expected changes in the investment's risk-return profile as per the CAPM. The formula for this stage computes the present value of dividends starting from year n. "DPS_n+1" can be calculated by multiplying the final DPS of the first stage (adjusted at g₁) by (1 + g₂). Alternatively, under the Two-Stage DDM's assumption that EPS and DPS grow at the same rate, "DPS_n+1" can also be determined by multiplying the final EPS of the first stage (also adjusted at g₁) by (1 + g₂) and then by the expected dividend payout ratio for the stable growth phase. In either approach, these future dividends are discounted to present value using the formula "DPS_n+1 / ((r_e,2 - g₂) * (1 + r_e,1)ⁿ)," effectively determining the value of dividends during the stable growth phase.

The sum of the present values from both stages yields P₀, the stock's estimated fair/intrinsic value. Therefore, to calculate the value using a Two-Stage DDM, one must discount the dividends of all the years of the extraordinary growth rate period plus the discounted value of dividends of the stable growth rate period. An in-depth example later in this article will explain how to locate and calculate these inputs for the Two-Stage DDM.

Assumptions of the Two-Stage Dividend Discount Model

The Two-Stage Dividend Discount Model (DDM) is grounded in key assumptions crucial for accurately assessing companies undergoing transitions in growth rates. These assumptions are vital in evaluating firms evolving from irregular to more sustainable growth:

• Extraordinary Growth Phase: The Two-Stage DDM begins with an "extraordinary growth phase," which, while generally characterized by higher growth rates, can also encompass scenarios of low or even negative growth. This period reflects the unique circumstances and challenges a company faces, be it aggressive expansion, market penetration, or restructuring efforts that might initially affect growth.
• Transition to Stable Growth: The model assumes that after the extraordinary growth phase, whether high, low, or negative, the company will transition to a period of stable and sustainable growth. The growth rate in this stable phase typically aligns more closely with long-term industry and economic averages, marking a shift from the initial, more variable growth period to a predictable and consistent growth trajectory.
• Variable Dividend Payout Ratio: In the Two-Stage DDM, the dividend payout ratio varies with the company's growth rate. During an extraordinary growth phase, a high growth rate typically corresponds to a lower payout ratio due to reinvestment needs. Conversely, a lower or negative initial growth rate might see a higher payout ratio. In the stable growth phase, the model anticipates a higher payout ratio if the initial growth was high, as the firm shifts from reinvestment to distributing more earnings as dividends. This reflects the lower reinvestment needs of a mature, stable company.
• Adjustment of Firm Characteristics in Stable Phase: In the stable growth phase, other characteristics of the firm, such as beta and return on equity, are expected to align with this new phase of stability. For instance, a high-growth firm might have a higher beta (indicating higher risk and potential return), which should adjust to a more moderate level as the firm enters its stable phase. Similarly, the return on equity, which might be elevated during the high growth phase, is expected to settle at levels typical for stable companies.

These foundational assumptions of the Two-Stage DDM are critical for its application to firms transitioning from an extraordinary to more sustainable growth rates. However, it's important to recognize that these assumptions may not be applicable to all companies, especially those with fluctuating growth patterns, changing dividend policies, or variable costs of equity. Accurate stock valuation using this model requires a thorough understanding and acknowledgment of these assumptions.

Relevant Applications of the Two-Stage Dividend Discount Model

The Two-Stage Dividend Discount Model (DDM) is particularly effective for analyzing companies at specific stages of their growth and dividend payout policies, as outlined below:

• Effective for Diverse Growth Phases: The Two-Stage DDM is ideal for companies experiencing varying growth patterns. It is especially effective for firms in high-growth phases expected to normalize (e.g., firms with valuable patents or in industries with significant entry barriers). The model is particularly applicable to firms with moderate initial growth rates, realistically capturing the transition from a higher to a more sustainable growth rate, such as from 10% to 5%.
• Mature Companies With Consistent Dividends: This model is well-suited for mature companies that have a history of consistent dividend payments and moderate growth rates. It accurately reflects the transition of these firms from their initial growth to a more established, stable phase.
• High Dividend Payout Ratios and Residual Cash Flow Distribution: The Two-Stage DDM is relevant for companies with higher dividend payout ratios, particularly those that distribute a significant portion of their residual cash flows as dividends. This feature is indicative of a company's transition from a phase of reinvestment to one where distributing earnings to shareholders becomes a priority.
• Objective Valuation and Dividend Policy Stability: The model's formulaic approach, based on present value concepts, minimizes subjectivity and enhances reliability in stock valuation. This is a shared advantage with general DDMs. Additionally, the Two-Stage DDM assumes dividend stability, crucial given that dividends are tangible and less likely to be manipulated. This stability is particularly important in the context of companies keen on maintaining steady dividend payments to avoid stock price volatility.

In summary, the Two-Stage DDM is distinguished by its adaptability to different growth scenarios, its applicability to mature firms with stable dividend records, and its relevance to companies with significant dividend payout ratios. These features, combined with its objective valuation approach and emphasis on dividend policy stability, make the Two-Stage DDM a versatile and reliable tool for stock valuation.

Limitations of the Two-Stage Dividend Discount Model

While the Two-Stage Dividend Discount Model (DDM) offers valuable insights in specific scenarios, it's essential to be aware of its limitations. These constraints become particularly relevant when applying the model to diverse market situations:

• Defining the Length of Extraordinary Growth Phase: One of the primary challenges is accurately determining the duration of the extraordinary growth period. The investment value in the model increases with the extension of this period, but translating qualitative assessments into a specific timeframe is complex and uncertain.
• Abrupt Transition to Stable Growth: The model's assumption of an immediate transition from extraordinary to stable growth at the end of the initial period is often an oversimplification. In reality, growth shifts, whether from high, low, or negative to stable, tend to occur more gradually. This gradual transition is better captured by models like the H-Model, which specifically address the nuances of these growth rate changes.
• Dividend-Centric Valuation Issues: The Two-Stage DDM's focus on dividends can lead to inaccuracies, especially for firms that do not distribute dividends in proportion to their earnings. It tends to underestimate the value of companies that retain earnings for reinvestment rather than paying out dividends, affecting the accuracy of the valuation.
• Predicting Future Dividend Growth: Forecasting future dividend growth during the initial fast growth stage is challenging. Typically, companies in this phase do not pay substantial dividends as they prioritize reinvesting earnings for growth, complicating the estimation of future dividend growth.

In summary, while the Two-Stage DDM is a useful tool for valuing stocks, particularly those transitioning from an extraordinary growth phase to a more stable period, it has its limitations. These include difficulties in accurately predicting the length of growth phases, unrealistic assumptions about growth rate transitions, and a focus on dividends that may not fully capture a company's true value. Consequently, it's advisable to use the Two-Stage DDM in conjunction with other valuation methods, acknowledging these limitations to gain a more comprehensive view of a company's worth.

Two-Stage Dividend Discount Model Example

For our example of valuing a dividend-paying company using the Two-Stage Dividend Discount Model (DDM), we'll use Comcast Corporation (CMCSA) as our case study. Comcast Corporation operates as a diversified media and technology company, primarily engaging in the operation of cable networks, broadcasting television stations, and providing internet and phone services. They also have a significant presence in the production and distribution of entertainment content through their ownership of NBCUniversal.

This is an appropriate company to use for the Two-Stage DDM due to several key reasons:

1. Rapid Dividend Growth Phase (2020-2023): Comcast has demonstrated significant annual dividend growth from 2020 to 2023, indicative of a high-growth phase, aligning with the first stage of the Two-Stage DDM.
2. Mature Market Presence: As a major player in the telecommunications and media industry, Comcast operates in a potentially maturing market, which may face challenges from market saturation and technology shifts, suggesting a transition to a lower, more stable growth phase suitable for the model's second stage.
3. Business Model and Industry Dynamics: Comcast’s diversified business model, spanning cable networks, broadcasting, internet services, and content production, positions it in an industry where initial high growth, driven by digital expansion and media consumption, could transition to stable growth as markets mature and evolve.

For applying the Two-Stage Dividend Discount Model to Comcast, we first gather the latest dividend payment (DPS₀) and earnings per share (EPS₀), representing the starting point for our analysis. Next, we identify the high initial dividend growth rate (g₁) from Comcast's rapid dividend growth between 2020 and 2023 and the lower, stable growth rate (g₂) for the subsequent stable phase. The model also requires two discount rates: r_e,1 for the initial high-growth phase and r_e,2 for the subsequent stable phase. Lastly, we'll determine the transition year (n), marking the shift from g₁ to g₂, to complete the necessary inputs for the Two-Stage DDM formula.

Step #1: Dividends Per Share (DPS₀) and Earnings Per Share (EPS₀)

This section discusses how you can find/calculate the current dividends per share (DPS₀) and earnings per share (EPS₀) in the Two-Stage DDM formula.

Dividends Per Share (DPS₀)

To determine the current dividend for Comcast, you can begin by examining their latest financial statements or press releases, which are accessible on their official website in the investor relations section. Furthermore, financial news websites and stock market analysis platforms frequently offer updated information on dividends for publicly traded companies such as Comcast. These resources will display the most recent dividend payment, known as the DPS₀ value, required for the Two-Stage DDM calculation.

According to the company's historical dividend information page, the company's 2023 annual dividend is $1.16, which will be our "DPS₀" in the Two-Stage DDM calculation.

Given the relationship between EPS and the DPR, you can also calculate the annual DPS as follows:

Annual Dividends Per Share (DPS) = Earnings Per Share (EPS) * Dividend Payout Ratio (DPR)

For instance, the EPS and DPR for Comcast are $3.76 and 30.85% respectively (calculated and defined below), which means the firm's annual DPS is $1.16 ($3.76 * 30.85%). This is an important calculation and relationship to keep in mind given its relevance in the Two-Stage DDM.

Earnings Per Share (EPS₀)

Earnings per share (EPS) represents the portion of a company's profit distributed to each outstanding share of common stock. Commonly located at the bottom of a company's income statement, EPS can also be calculated as follows:

Earnings Per Share (EPS) = (Net Income - Preferred Dividends) / Weighted Average Shares Outstanding

If we use trailing twelve month (TTM) numbers, we can calculate Comcast's current earnings per share:

Earnings Per Share (EPS) [CMCSA] = ($15,152M - $0M) / 4,025M --> $3.76

This $3.76 will therefore be our "EPS₀" in the Two-Stage DDM calculation.

Step #2: Extraordinary Dividend Growth Rate (g₁)

To determine a company's extraordinary growth rate (g₁), it's common practice to evaluate the average growth rate during a previous period of high growth. This assessment may involve computing a simple average of the year-over-year growth rates or employing the compound annual growth rate (CAGR) for a time frame when the growth significantly exceeded the norm.

For illustration purposes, I've collected dividend data for Comcast from 2008 to 2023, as shown below:

To find Comcast's extraordinary growth rate (g₁) for the Two-Stage DDM, we examine the more recent and stable growth rates from 2021 to 2023, which indicate a steady growth of about 8-9.5%. The CAGR calculation is preferable for consistent growth analysis over multiple years.

For reference, the formula for CAGR is shown below:

CAGR = [(Ending Value / Beginning Value)^{(1 / Number of Years)}] - 1

However, since we are focusing on a short and recent period where the growth rate has been relatively stable, a simple average of these rates suffices and reflects the company's current growth phase. Calculating the average growth rate for these years (8.9%, 8.2%, and 9.4%) results in a g₁ of 8.8%, which mirrors Comcast's current extraordinary dividend growth trend.

Step #3: Perpetual Dividend Growth Rate (g₂)

To estimate the perpetual dividend growth rate (g₂), which forecasts the continual increase of dividends indefinitely, you can utilize the two methods outlined in this section. Additionally, it's crucial to follow two guidelines: (1) keeping this rate below the nominal growth rate in the firm's economy, and (2) ensuring that both the dividend payout ratio and return on equity align with the estimated perpetual dividend growth rate during the firm's stable phase.

For a more comprehensive understanding, I recommend reading my article on estimating the perpetual dividend growth rate. It offers additional methods beyond those discussed here and delves deeper into these topics.

Method #1: Historical Dividend Growth Rates

To estimate a company's perpetual dividend growth rate, a useful strategy is to examine its past growth rates, especially over a period of 5+ years or more. This method highlights long-term tendencies and current dividend growth trends, essential for evaluating the company's present financial health.

Considering the fluctuation in the company's dividend growth in the past ten years, a CAGR calculation spanning the last 8 to 10 years would be beneficial to discern the true growth of dividends. The following table illustrates this:

In short, by examining the company's dividend CAGR over an extended period of 8-10 years and assuming this trend persists, we can anticipate the firm's perpetual dividend growth rate to lie between 2-6%. To be conservative, we'll assume the 8-year 2.13% growth rate is reasonable.

Method #2: Sustainable Dividend Growth Rate

The sustainable dividend growth rate serves as a practical measure for determining how much a company can boost its dividends consistently without seeking additional external capital. This metric is particularly beneficial for the Two-Stage DDM, as it takes into account the firm’s earnings and the share of profits paid out as dividends. It's also a highly recommended method for this model, given its relationship with return on equity and the dividend payout ratio, which can be utilized to estimate the firm's stable period dividend payout ratio, as discussed later. Typically, this yields a growth rate grounded more firmly in the company's real financial outcomes, as opposed to basing it purely on historical trends.

The sustainable dividend growth rate formula is shown below:

Sustainable Dividend Growth Rate = ROE * (1 - (DPS / EPS))

where:

• ROE = return on equity (net income / shareholders' equity)
• DPS = annual dividend per share
• EPS = earnings per share ((net income - preferred dividends) / weighted average outstanding shares)

In this formula, return on equity (ROE) quantifies a company's profit generation from shareholder equity, reflecting efficiency. Conversely, the dividend payout ratio (DPS/EPS) indicates the earnings proportion distributed as dividends. The sustainable dividend growth rate formula therefore projects achievable growth without additional funding, assuming the company reinvests its retained earnings at its existing ROE level. This reinvestment is anticipated to drive future growth by effectively utilizing retained profits to generate additional earnings.

Using trailing twelve month (TTM) numbers from Comcast's financial statements, we'll calculate the firm's sustainable dividend growth, as shown below:

Sustainable Dividend Growth Rate [CMCSA] = 7.88% * (1 - ($1.16 / $3.76)) --> 5.45%

The FY 2022 sustainable dividend growth rate calculation for Comcast indicates a possible perpetual dividend growth rate of 5.45%, which is lower than our anticipated extraordinary growth rate of 8.8%. This rate provides a practical viewpoint for the Two-Stage DDM, linking dividend growth closely with Comcast's current earnings generation and distribution capabilities, thereby presenting a more grounded estimate of sustainable growth.

Guideline #1: Align Perpetual Dividend Growth With Economy's Growth Rate

In the Two-Stage DDM, the dividend growth rate (g₂) must be lower than the discount rate (r_e,2) to avoid unrealistic valuations. It should also not exceed the economy's growth rate where the firm operates. To ensure this, you can:

1. Cap at Economy's Growth Rate: Restrict the dividend growth rate to match the economy's growth rate, with a possible allowance of 1-2% above it if the model supports it. This approach aligns the firm's growth with the broader economic environment, ensuring that the projections don't unrealistically outpace the market's overall capacity for growth.
2. Risk-Free Rate as Benchmark: Employ the 10-year U.S. Treasury Note interest rate as a cautious benchmark for the growth rate. This method anchors the growth rate to a widely recognized standard of minimal risk, providing a more cautious and grounded estimate which is particularly useful in uncertain or volatile market conditions.
3. Combine Inflation and Economic Growth: Integrate long-term inflation expectations with the average economic growth rate for a more comprehensive view. This method accounts for both the general increase in prices over time and the economic environment's potential for expansion, offering a balanced approach to forecasting future growth.

These methods are standard in all dividend discount models (DDMs) to ensure a realistic growth rate, recognizing that no company can perpetually exceed the economy's growth or the risk-free rate.

For Comcast, one method yielded a perpetual dividend growth rate estimate of 2.16%, and the second method suggested a rate of 5.45%. Given that the average 10-year GDP growth rate in the U.S. is 2.40%, and to be more conservative, we'll use 2.16% as our final perpetual dividend growth rate (g₂).

Guideline #2: Align DPR and ROE With Stable Phase

In the Two-Stage DDM, a crucial factor for accurate valuation is the alignment of the dividend payout ratio (DPR) and return on equity (ROE) with the company's stable phase. This is essential as companies transition from their initial growth phase, which can vary in intensity, to a more stable phase. This relationship is explained below for the DPR and ROE:

• Dividend Payout Ratio (DPR): The DPR reflects the company's ability to distribute cash to shareholders and varies inversely with its growth rate demands. Therefore, in a scenario where the initial growth phase is high, the stable phase often permits a higher DPR due to decreased reinvestment needs. Conversely, if the initial growth is low or negative, the stable phase might see a comparatively lower DPR, as the initial phase may already involve higher payouts.
• Return on Equity (ROE): ROE measures a company's profitability by assessing how efficiently it generates net income relative to its shareholders' equity. During a high-growth phase, ROE might be elevated due to the benefits of reinvesting earnings, but it tends to normalize in the stable phase. Conversely, in cases where the initial growth is low or negative, the ROE during the growth phase might be lower and could increase as the company stabilizes. This shift in ROE indicates the company's transition to a more consistent growth trajectory.

In essence, these changes in DPR and ROE in the Two-Stage DDM are indicative of a company's progression from its unique growth phase to a more stable and predictable operational phase, and the relationship can be reversed depending on the nature of the initial growth phase.

Now, the conventional approach to estimating this new dividend payout ratio is to use the sustainable growth rate method, which we applied in method #2 above, yielding a perpetual dividend growth rate of 5.45%. However, since we have already determined that the 2.16% rate (from method #1 above) is more reasonable and conservative, we'll use this rate instead.

Then, you'd use the formula below to estimate the firm's stable dividend payout ratio:

Stable Dividend Payout Ratio = 1 - (Stable Growth Rate / Stable Period ROE)

We have the stable growth rate (2.16%), but what remains to be determined is the stable period ROE. Estimating this requires some analysis on your part, for which the industry average return on equity could provide guidance.

In our case, considering that Comcast's trailing twelve months (TTM) ROE is 7.88%, which is already relatively low, we'll assume a decline to 6.0% in the stable phase. This assumption lets us determine the firm's stable dividend payout ratio, as calculated below:

Stable Dividend Payout Ratio [CMCSA] = 1 - (2.16% / 6.0%) --> 64.0%

Therefore, we're estimating the firm's DPR in the stable phase to be 64.0%, which is rightfully above its TTM DPR of 30.1%.

In conclusion, these formulas and considerations help in determining a more accurate and sustainable dividend payout strategy, especially during the transition from growth to stability. The goal is to ensure that the firm's dividend policy is in line with its long-term growth prospects and financial health.

Step #4: Discount Rates (r_e,1, r_e,2)

The discount rate (aka required rate of return), is predominantly derived from the Capital Asset Pricing Model (CAPM). Central to calculating the present value of future cash flows in dividend discount models, CAPM illustrates the proportional relationship between the risk of an investment and its anticipated return. It suggests that increased risks necessitate higher returns. This model is crucial in evaluating the impact of market risks on investment valuations and projected returns.

The CAPM formula is shown below:

r_e = r_f + β*(r_m - r_f)

where:

• r_e = cost of equity
• r_f = risk-free rate
• β = beta
• r_m = expected market return

Solving for the cost of equity (r_e) provides the discount rate needed for use in your present value DDMs.

Locating the three inputs to the CAPM for Comcast is fairly straightforward:

• Risk-Free Rate (r_f): The risk-free rate is typically represented by the interest rate on the 10-year U.S. Treasury Note, selected for its status as one of the safest investments. Backed by the U.S. government, it carries minimal risk of default. This rate acts as a foundational benchmark for evaluating the risk of more speculative investments. Currently, this rate stands at 4.37%.
• Beta (β): Beta measures the volatility of a stock in comparison to the overall market, denoting systematic risk, which is the risk inherent to the whole market or a specific market sector. A beta above 1 suggests higher volatility than the market, and a beta below 1 indicates lower volatility. Beta values for individual companies, like Comcast, are accessible on financial platforms such as Yahoo Finance, listed as "Beta 5Y Monthly." Comcast's 5-year monthly beta is currently 1.06.
• Expected Market Return (r_m): The expected market return often utilizes a standard value of 10%, mirroring the historical average annual return of broad market indices, such as the S&P 500. This rate serves as a general guide for what investors might anticipate as the market's average yield over an extended period.

Using these inputs, we can calculate the CAPM for Comcast:

r_e,1 [CMCSA] = 4.37% + 1.06*(10% - 4.37%) --> 10.34%

With a CAPM result of 10.34% for Comcast, this figure symbolizes the anticipated return on investment, taking into account the relevant risk elements and market forecasts. It implies that investments in Comcast should target a minimum return of this rate to compensate for the perceived risks. This 10.34% is the "r_e,1"​ in the Two-Stage Dividend Discount Model (DDM) calculation, representing the discount rate during the initial extraordinary growth phase.

Now, to determine the cost of equity in the stable phase (r_e,2), the CAPM formula remains relevant. However, it's prudent to modify the CAPM inputs to reflect the company's evolving risk-return profile. The three components of the CAPM (r_m, r_f, and β) should be considered for these adjustments, as described below:

• Risk-Free Rate Adjustments: The risk-free rate, reflecting broader economic conditions like monetary policies and inflation rates, is a macroeconomic factor not specific to individual companies. Predicting changes in the risk-free rate is challenging due to its susceptibility to unpredictable economic and political events. Therefore, in CAPM calculations, the risk-free rate should be based on current and historical trends, rather than speculative future changes, to ensure a realistic and well-grounded cost of equity estimation.
• Beta Modification: Reassessing the company's beta, which measures stock volatility relative to the market, is crucial. As companies transition to less risky and more predictable operations in the stable phase, a lower beta, typically between 0.8 and 1.2 for stable companies, is appropriate. This lower beta reflects reduced volatility and risk, thereby decreasing the cost of equity. Conversely, a higher beta might be warranted if a company faces increased market volatility or adopts riskier strategies, increasing the cost of equity. This adjustment ensures that the CAPM calculation accurately reflects the company’s risk profile during its stable growth phase.
• Market Return Expectation Changes: Fluctuations in market return expectations, influenced by changing market conditions or economic outlooks, have significant implications for the cost of equity. A decrease in expected market returns, perhaps due to a bearish outlook or slowing economic growth, would lead to a lower cost of equity. Conversely, an increase in expected market returns, signaling stronger market growth, would raise the cost of equity.

Thus, when adjusting the CAPM for Comcast's stable phase, it's reasonable to estimate a decrease in beta to 0.95 (from its current 1.06). This adjusted beta would be used to recalculate the CAPM, resulting in a revised cost of equity (r_e,2) for the stable growth phase.

Using this new estimated beta to calculate the CAPM for the stable growth phase would yield the following result:

r_e,2 [CMCSA] = 4.37% + 0.95*(10% - 4.37%) --> 9.72%

In Comcast's case, the cost of equity, calculated using the CAPM for the stable growth phase of the Two-Stage DDM, amounts to 9.72%. This 9.72% figure is then utilized as the "r_e,2" input for the Two-Stage DDM calculation.

• Related: How to Calculate and Interpret the Capital Asset Pricing Model (CAPM)

One final note to consider is that while CAPM is the most conventional method for estimating a company's discount rate in the Two-Stage DDM, it's not the only approach. Other methods, such as simply using your personal required rate of return for the company, may also be employed to cross-verify or gain a more nuanced understanding of a company's risk and return profile.

Step #5: Transition Year (n)

Determining the transition year (n) in the Two-Stage DDM is important, as it represents the final year of the first-stage dividend growth period, after which the dividend growth rate shifts to a more sustainable, stable rate. This transition point from an extraordinary growth rate (g₁) to a perpetual growth rate (g₂) is key to accurately valuing a stock using this model.

To determine "n" for a specific company, consider the following factors:

• Company's Growth Phases: Understand the company's current position in its growth lifecycle. Evaluate if it's in an early high-growth phase, transitioning phase, or a mature stable phase.
• Industry and Market Trends: Consider the industry and overall market conditions. Some industries have longer growth phases than others.
• Company's Future Plans and Projections: Look at the company's strategic plans, projected earnings, and expected changes in operations or markets. These can provide insights into how long the current growth rate is sustainable.
• Historical Growth Periods: Analyze the duration of past growth phases for the company and similar companies in the industry to get a benchmark.

For Comcast, you would gather data on its past growth periods, industry growth norms, and any strategic plans or forecasts provided by the company. Based on this information, you can estimate when Comcast is likely to transition from its current growth phase (reflected by g₁ and r_e,1) to a more stable growth phase (reflected by g₂ and r_e,2).

In our case, Comcast has maintained a relatively high dividend growth rate over the past five years. However, due to a less optimistic outlook on the company's industry and market trends, coupled with a higher dividend payout ratio expectation of 64.0% after the initial extraordinary growth phase (indicating limited room for further dividend growth), we'll assume that the transition to the stable growth rate commences at the beginning of 2026. This decision implies an "n" value of 2 years in the Two-Stage DDM calculation.

Step #6: Calculate and Interpret the Two-Stage DDM

Now that we have all the inputs, we can calculate the Two-Stage DDM for Comcast (CMCSA). To simplify the calculation, let's start by determining the value of extraordinary growth:

Next, we calculate the value of stable growth. To calculate "DPS_n+1" we can either (1) simply grow the annual DPS, or (2) grow the EPS and multiply it by the expected stable dividend payout ratio (of 64.0%) to estimate future dividends. The first approach is shown below:

Here's the second approach to calculate the present value of stable growth:

Clearly, the assumption that EPS grows at the same rate as DPS, combined with a stable phase DPR of 64.0%, significantly affects our present value calculation for Comcast's stable growth phase. Assuming our estimates are reasonable, we'll adopt the V2 calculation from above ($31.62), as our final present value calculation for the stable growth phase.

By summing the present value of extraordinary growth and the present value of stable growth, we can derive Comcast's intrinsic value according to the Two-Stage Model, which totals $33.89 ($2.27 + $31.62). If we were to plot the company's dividends and dividend growth according to this model over a 15-year span, here's what it would look like:

Now, in terms of interpretation, the Two-Stage DDM calculates Comcast's intrinsic price at $33.89, while its current stock price is ~$44.64. This suggests the stock is overvalued, given that the intrinsic share price is lower than its current stock price.

Furthermore, by applying a 20% margin of safety, a modest yet reasonable figure considering the uncertainties and assumptions inherent in both the company and the model, we can determine the actual buy price for the company. This adjustment establishes the buy price at $27.11 ($33.89 * (1 - 0.20)), further emphasizing the overvaluation of Comcast's stock.

Lastly, conducting a sensitivity analysis is essential for precise valuations due to the Two-Stage DDM's dependence on input variables. An iterative data table is an effective tool for this, allowing for the analysis of minor variations in two sensitive inputs of the Two-Stage Model. In this instance, we'll examine how small adjustments to the perpetual dividend growth rate and variations in the margin of safety influence the buy price.

The data table below demonstrates how small, incremental changes of just 0.25% to the perpetual dividend growth rate (2.16%), and a more moderate adjustment of 2.5% to the margin of safety (20%), can affect Comcast's buy price:

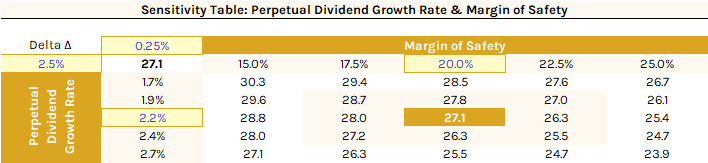
Ultimately, the practice of conducting a sensitivity analysis, as demonstrated above, highlights the critical importance of factors such as carefully selecting the appropriate company, accurately estimating discount rates, making informed choices regarding dividend growth rates, and setting a prudent margin of safety. These factors wield a significant influence on our comprehension of a company's valuation. As a result, this comprehensive approach is strongly recommended for the precise application of the Two-Stage DDM.

The Bottom Line

The Two-Stage Dividend Discount Model (DDM) is an advanced valuation method that assesses a stock's intrinsic value by accounting for two distinct dividend payout phases: an initial period of extraordinary growth, followed by a stable growth phase into perpetuity. This model is particularly suited for companies transitioning from rapid growth to a more stable phase, showcasing its adaptability to varying growth rates, mirroring a company's dynamic lifecycle.

However, the Two-Stage DDM does rely on certain assumptions and comes with limitations. It presupposes an immediate transition between growth phases and continuous dividend payments, while precise estimations of growth rates, dividend ratios, and discount rates can be complex due to company and market uncertainties. Despite these challenges, the Two-Stage DDM remains a valuable tool for investors, offering nuanced valuations, especially for companies experiencing shifts in their growth patterns.