In this article, I will show you how to calculate and interpret stock and portfolio beta. Beta, as a measure of a stock or portfolio's volatility relative to the market, offers valuable insights into implied risk for investors. We'll explore the formula for calculating beta and provide detailed, step-by-step instructions on computing and interpreting this figure in Excel for both individual stocks and portfolios. Additionally, we'll cover the concepts of levered versus unlevered beta and discuss the drawbacks of using beta. This knowledge is valuable, as beta is a key element in numerous financial models and indicates the volatility risk in stocks and portfolios.

Understanding Beta

Beta, represented by the Greek symbol β, describes the relationship between the returns of a stock and the returns of the overall market.

Beta measures the movement of a stock's price in relation to a broader market index, such as the S&P 500 Index. This relationship is observed over a specific period and can be depicted by the slope of a line on a scatter plot.

This concept is illustrated in the beta chart shown below:

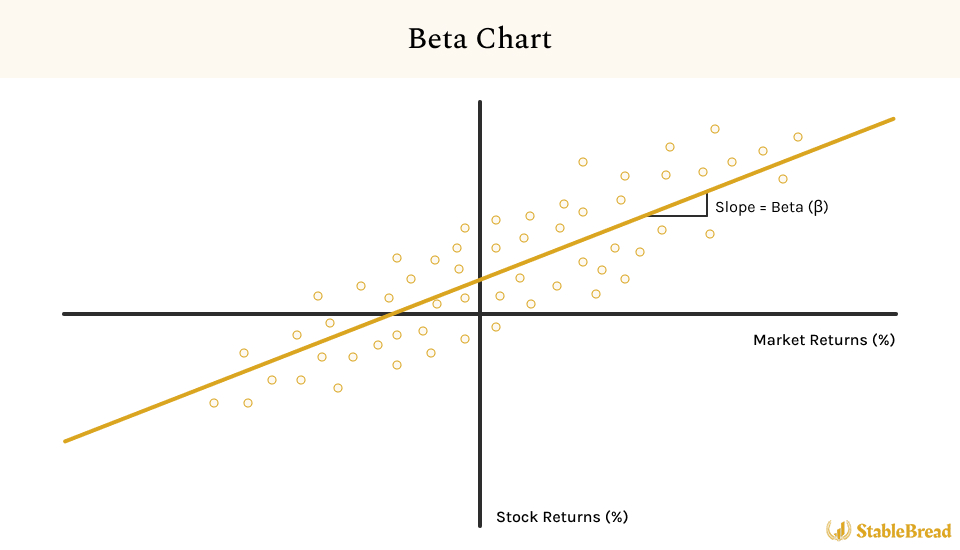
In this plot, the horizontal axis represents the percent change in the overall market's value, while the vertical axis corresponds to the percentage change in the stock price. The plotted data points reflect specific instances of market and stock performance over time, allowing for a direct comparison of the stock's returns to those of the market. Determining beta involves calculating the line of best fit through these data points, which visually represents the stock's responsiveness to market changes.

How to Interpret Beta

Because beta is simply the slope of this line, it can be positive, zero, or even negative, each indicating a different level of volatility and market correlation.

Once beta is found, it can be interpreted in the following ways:

• Beta > 1.0: Indicates higher volatility than the market, with high correlation. For example, a market return of 10% and a stock return of 20% results in a beta of 2.0, common in sectors like Technology.
• Beta = 1.0: The stock's volatility matches the market, showing perfect correlation. An example is when both the market and stock return 10%, leading to a beta of 1.0.
• Beta Between 0 and 1.0: Represents lower volatility compared to the market, with slight correlation. For instance, a market return of 10% and a stock return of 7% yields a beta of 0.7, typical in stable industries like Utilities.
• Beta = 0: Shows no correlation with the market and significantly lower volatility. For example, a constant stock return with fluctuating market return results in a beta of 0, often in non-cyclical sectors.
• Beta Between -1 and 0: Indicates negative correlation with the market and lower relative volatility. A typical case is when the market rises by 10% and the stock falls by 5%, leading to a negative beta.
• Beta = -1.0: Demonstrates perfect inverse correlation with the market, with equal volatility. For example, a 10% market increase and a 10% stock decrease results in a beta of -1.0.
• Beta < -1.0: Shows higher volatility and strong inverse correlation compared to the market. An example is when the market rises by 10% and the stock falls by 15%, resulting in a beta lower than -1.

In conclusion, understanding the range of beta values helps investors gauge a stock's relative risk and potential behavior under different market conditions, thus serving as a critical tool in portfolio management and investment strategy formulation.

Systematic vs. Unsystematic Risk

There are two fundamental types of risks that concern market participants: systematic and unsystematic risks. Understanding these risks is important for interpreting beta accurately.

Here are the key differences between the two risks:

• Systematic Risks: These refer to risks that impact the entire market or a significant portion of it, often resulting from external, economy-wide factors such as economic recessions, political instability, interest rate fluctuations, and global events. Systematic risk cannot be diversified away and affects a wide range of assets across the market.
• Unsystematic Risks: These are risks specific to a particular company or industry, arising from internal or sector-specific factors. Elements such as company management decisions, financial practices, industry trends, and operational factors fall under this category. Unlike systematic risk, unsystematic risk can be mitigated through a well-balanced and diversified portfolio. This approach is crucial in individual stock selection and sector allocation, as it helps reduce the impact of adverse events on a single company or industry within the overall portfolio.

Beta, as a measure of a stock's volatility relative to the market, primarily gauges systematic risk. It indicates how a stock's returns move in tandem with broader market movements, thus capturing the sensitivity of the stock to prevailing market forces. Understanding both systematic and unsystematic risks, and how beta relates to them, allows investors to construct portfolios that align with their risk tolerance and investment objectives.

How to Calculate Beta

Calculating the beta of a stock is essential for evaluating its risk relative to the market. Beta gauges how a stock's returns correlate with the market's movements, which is what its formula reflects.

Beta can be calculated using the formula below:

β = Covariance (R_e, R_m) / Variance (R_m)

where:

• β = beta
• R_e = return on individual stock
• R_m = return on overall market
• Covariance = stock's return relative to the overall market
• Variance = how the market moves relative to its mean

The beta calculation involves dividing the covariance of a stock's returns with the market's returns by the variance of the market's returns. Covariance measures how the stock's returns move in relation to the market's, indicating whether they tend to increase, decrease, or stay neutral as the market changes. Variance, on the other hand, represents the fluctuation of the market's returns around its average. Thus, beta quantifies the stock's relative volatility.

How to Calculate Stock Beta in Excel

To calculate the beta of a stock in Excel, you'll need to perform a regression analysis, assessing the relationship between the stock's performance and that of the overall market.

Here's a finished Excel beta calculation spreadsheet you can download for the company Microsoft (MSFT), which mirrors the steps and explanations shown further below:

Step #1: Gather Historical Data

Begin by sourcing the historical closing prices for both the stock and a market index, like the S&P 500, over an identical period. Reliable historical price data can be obtained from various sources, Yahoo Finance being one popular option.

When collecting this historical data, consider the following key aspects:

• Market Index Selection: The choice of index is crucial, as beta is calculated relative to a specific market. Different indices can yield different beta values due to their unique compositions and characteristics.
• Time Frame Consideration: The length of the time frame used for analysis can affect the results. Shorter periods, such as less than a year, might reveal more volatility, while longer periods, like five years or more, tend to offer a more stable view. The standard recommendation is a 5-year period for a balanced analysis.
• Time Interval Selection: Deciding on time intervals (daily, weekly, or monthly) is significant, as it dictates the analysis's granularity and variability. Shorter intervals can provide detailed insights but may include more noise, whereas longer intervals smooth out short-term fluctuations but could overlook finer movements.

In short, these considerations are fundamental in ensuring the accuracy and relevance of your beta calculation.

Step #2: Organize Data in Excel

After you've gather the historical data over the same time period for the stock and the market index, it's advisable to arrange your data in the following columns:

At this stage, your spreadsheet should only include columns A, B, and C, which will contain the dates, and the closing prices of the market and stock, respectively. Make sure the dates in column A are sorted from the oldest to the newest.

Step #3: Calculate Percent Returns

Now, it's time to calculate the percent returns for columns [D] and [E], based on your selected time interval, whether it be daily, weekly, or monthly. To accomplish this, just use the percent change formula:

Percent Change = ((New Value / Old Value) - 1) * 100

where:

• New Value = value at the later time period (t),
• Old Value = value at the earlier time period (t - 1).

This formula calculates the percentage change in value from one time period (t - 1) to the next (t), providing a transparent view of how the value has changed over time. Make sure to apply this formula to each row, except for the first row, as it lacks a preceding period for comparison.

Step #4: Calculate Beta

There are three primary methods for calculating beta in Excel. The choice of method ultimately doesn't impact the end result of obtaining the beta value.

Method #1: Slope Function

Because beta is represented by the slope of the regression line in a scatter plot, where the line's angle indicates the stock's responsiveness to market changes, the simplest method to calculate beta in Excel is to utilize the SLOPE function. In this context, the SLOPE function effectively determines the gradient of the line that best fits the relationship between the stock's returns and the market's returns.

The Excel formula for this would be =SLOPE([E], [D]), where [E] represents the range of the stock's returns and [D] represents the range of the market's returns. This function calculates the beta directly, reflecting how much the stock's returns change for each unit change in the market's returns.

Method #2: Covariance and Variance Functions

The second method involves directly solving for beta using its formula. In Excel, you should employ the sample covariance and variance functions, namely COVARIANCE.S and VAR.S, for this calculation. These functions are adept at estimating covariance and variance from a sample, which aligns well with the nature of financial data such as stock prices, typically considered a representative sample of broader market activity.

Referring to the earlier mentioned beta formula, begin by calculating the covariance between the stock's returns (R_e) and the market's returns (R_m). In Excel, this is achieved with the formula =COVARIANCE.S([D], [E]), where [D] represents the range of market returns and [E] represents the range of stock returns. The subsequent step involves determining the variance of the market returns (R_m), which is done using =VARIANCE.S([D]) in Excel. Finally, dividing the calculated covariance by the variance gives you the stock's beta, offering a quantitative measure of its relative volatility compared to the market.

Method #3: Regression Analysis

The final method for calculating beta involves using regression analysis, which, although the most involved process, offers a comprehensive statistical approach. This method leverages historical data to establish a relationship between the stock's returns and the market's returns. By fitting a regression line to these data points, it determines the slope, which represents beta. This slope indicates how much the stock's returns are expected to change for a given change in the market's returns, providing a nuanced view of the stock's market sensitivity.

To conduct a regression analysis in Excel, first ensure that the "Data Analysis" Excel ToolPak is installed. Then, follow these steps:

1. Go to Data --> Data Analysis --> Regression --> OK.
2. For "Input Y Range", select the dependent variable, which is the returns column for the stock ([E]).
3. For "Input X Range", select the independent variable, which is the returns column for the market ([D]).
4. Check "Labels" if your column selections include labels, and choose a location for the output of your regression analysis.
5. Leave all other boxes/selections as default. Finally, click on the "OK" button.

Once the regression is complete, you should see a summary output similar to the example below (excluding the formatting):

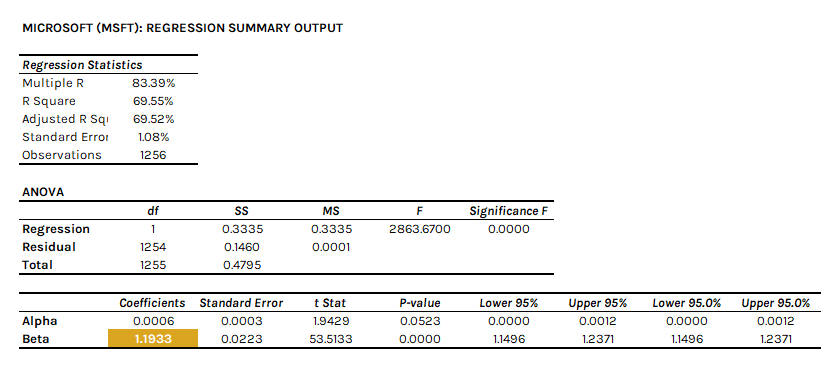
As shown, the beta for MSFT in this regression analysis is 1.933. Additionally, the output provides the alpha, p-values, r-squared, standard error, number of observations, and other statistical measures. These are valuable for broader investment analysis, including portfolio evaluation and risk assessment.

Step #5: Interpret Stock Beta

If you reference my completed beta Excel workbook from above, you'll see a chart that looks similar to the one below:

The given formula, "y = 1.1933x +0.0006," represents the regression equation for Microsoft's (MSFT) stock returns relative to the S&P 500 Index over the past five years, using daily closing prices. In this equation, the beta value for Microsoft is 1.1933. This indicates that Microsoft's stock is more volatile than the market: it tends to move approximately 19.33% more than the market for every percentage change in the S&P 500. The constant term, 0.0006, or alpha, represents the stock's expected return independent of the market's movements. However, in practical terms, this alpha value is very small and suggests minimal return not explained by the market's movements.

How to Calculate Portfolio Beta in Excel

Calculating the beta of a portfolio is essential for understanding its overall risk in relation to the market. By understanding your portfolio's beta, you can make informed decisions about risk management and asset allocation.

This process, akin to calculating stock beta in Excel as demonstrated earlier, requires more extensive data gathering, organization, and calculations. It involves determining the weights of each security in the portfolio and then calculating the weighted average of the betas of the individual securities within the portfolio.

Here's a finished Excel portfolio beta calculation spreadsheet you can download, which mirrors the steps and explanations shown further below. Microsoft (MSFT), Apple (AAPL), and Johnson & Johnson (JNJ) are the three securities in this portfolio example.

Step #1: Gather Historical Data

This step mirrors step #1 used for the stock beta example above. The main difference is that you'll be sourcing historical closing prices for all the stocks in your portfolio, rather than just one stock and a market index.

The previously discussed aspects, including market index selection, time frame consideration, and time interval selection, remain important, particularly when assessing your portfolio's beta. For instance, if you only have one year of performance history for your stocks, it may not be practical to use a 5-year lookback period for beta calculation. Aligning these key aspects with your available data is crucial to ensure the accuracy and relevance of the beta calculation across your entire portfolio.

Step #2: Organize Data in Excel

Once you've collected the historical data for the stocks in your portfolio and the market index over the same time period, it's recommended to organize your data into the following columns, assuming your portfolio comprises three stocks:

At this point, your spreadsheet should only have columns A, B, C, D, and E filled out, containing just the dates, market prices, and relevant stock prices. Ensure that the dates in column A are sorted from the oldest to the most recent.

Step #3: Calculate Percent Returns

Now, you should calculate the percent returns for columns [F], [G], [H], and [I], depending on your chosen time interval, which could be daily, weekly, or monthly. To do this, apply the percent change formula used previously: ((New Value / Old Value) - 1) * 100.

Step #4: Calculate Beta for Every Security

You have the option to use any of the three methods previously discussed for calculating stock beta to determine the beta for each security in your portfolio. For simplicity, I recommend using the SLOPE function in Excel.

In Excel, the formula =SLOPE([Stock Returns Range], [Market Returns Range]) is used for this calculation. In this context, [Stock Returns Range] corresponds to the return ranges for each stock in your portfolio, located in columns [G], [H], or [I]. Column [F] consistently represents the market's returns within the formula. This arrangement facilitates the calculation of the relationship between each stock's returns and the market's returns, thus effectively determining the individual beta values for each stock in your portfolio.

Step #5: Determine Portfolio Weights

The next step involves calculating the weight of each security in your portfolio. While most investment brokerages readily provide these percentages, including individual stock weights and the total portfolio market value, you can also compute them manually.

This is done by dividing the market value of each security by the total market value of the portfolio. The formula for this calculation is as follows:

Security Weight = (Security's Market Value) / (Total Portfolio Market Value)

where:

• Security's Market Value: Current stock price * number of shares owned. For instance, if you own 100 shares of a stock priced at $50 each, the market value is $5,000.
• Total Portfolio Market Value: Sum of the market values of all securities in the portfolio. For example, if your portfolio includes stocks valued at $5,000, $3,000, and $2,000, the total is $10,000.

Step #6: Calculate Portfolio Beta

The final step in calculating the portfolio beta involves multiplying the beta of each security by its respective weight and then summing these products for all securities in the portfolio, as shown in the formula below:

Portfolio Beta = ∑(Beta of each security * Weight of each security)

You can use the SUMPRODUCT function in Excel for this calculation. In a separate cell, enter: =SUMPRODUCT(Beta Range, Weight Range). Here, "Beta Range" refers to the cell range containing the betas of the individual securities, and "Weight Range" refers to the cell range containing their respective weights.

Step #7: Interpret Portfolio Beta

Referring to the completed portfolio beta Excel workbook provided above, you'll find a calculated beta of 0.9552. This figure is for a portfolio comprising MSFT, AAPL, and JNJ, measured against the S&P 500 Index over a 5-year period using daily closing prices. The respective assumed weights of these stocks in the portfolio are 42%, 21%, and 37%.

To interpret this beta of 0.9552, it suggests that the portfolio has a volatility slightly below the market average. Being close to 1, it indicates that the portfolio generally moves in tandem with the market, as represented by the S&P 500 Index. However, its value slightly less than 1 implies that it is a bit less reactive to market fluctuations than the market itself, reflecting a balanced risk profile that aims to capture market gains while moderately reducing volatility.

Understanding Levered and Unlevered Beta

When you calculate beta or find it listed for a publicly traded stock, you're typically looking at levered beta. Levered beta (β_L​), also known as equity beta, reflects the volatility of a stock, including the impact of the company's capital structure (its mix of debt and equity).

However, to compare companies on a more equal footing, particularly across different industries or with varying levels of debt, you might want to calculate unlevered beta (β_U​), also known as asset beta. Unlevered beta strips out the effects of financial leverage and shows the company's risk in relation to the market independent of its debt levels.

Understanding both levered and unlevered beta provides a more nuanced view of a company's risk profile, offering insights into how much of its volatility is due to the market and how much is due to its capital structure.

How to Calculate Unlevered Beta

Unlevered beta removes the impact of debt from the company's risk profile. This calculation is valuable for comparing the risk of companies across different industries or with different capital structures, as it isolates business risk from financial risk.

The formula for converting levered beta to unlevered beta is shown below:

β_U = β_L / (1 + D/E * (1 - T_c))

where:

• β_U = unlevered beta
• β_L = levered beta
• D = value of debt
• E = value of equity
• T_c = corporate tax rate​​

In this formula, levered beta (B_L) can be sourced online or calculated using one of the previously discussed methods. The total debt (D) is located in the company's balance sheet, part of its financial statements. The market capitalization, or total market value of the company's equity (E), is calculated by multiplying the current stock price with the total number of outstanding shares. The corporate tax rate (T_c), the rate at which the company's profits are taxed, can be found in the company's financial reports, typically in the notes to the financial statements, or by looking up the prevailing corporate tax rates in the company's country of operation.

Investors and analysts often calculate unlevered beta to understand the intrinsic, operational risk of a business without the influence of its financing decisions. This is especially helpful when valuing companies that are significantly different in terms of debt structure or when assessing the risk of a business sector as a whole.

How to Calculate Levered Beta

For private companies or projects without a readily available beta, analysts might use the unlevered beta of similar public companies and then re-lever it according to the private company's capital structure. This approach helps in estimating the expected return or cost of equity for the private entity, considering its unique financing mix.

Levered beta takes into account the company's debt, effectively combining its market risk with the risk introduced by its specific capital structure.

The formula for converting unlevered beta to levered beta is shown below:

β_L = β_U * (1 + D/E * (1 - T_c))

where:

• β_L = levered beta
• β_U = unlevered beta
• D = value of debt
• E = value of equity
• T_c = corporate tax rate

This method is useful for understanding a company's market-related risk combined with its financial risk due to leverage. Further, levered beta is particularly useful when analyzing companies with different capital structures or for assessing the risk of equity in a leveraged company.

Drawbacks of Beta

Beta is widely used in finance theory and models, such as in the Capital Asset Pricing Model (CAPM), but comes with a number of drawbacks that are worth mentioning:

1. Historical Data Reliance: Beta depends on historical market data, assuming that past stock volatility is a reliable indicator of future risks.
2. Volatility Misinterpretation: It equates volatility with risk, which may not fully represent true investment risks like permanent capital loss or return uncertainty.
3. Short-Term Focus: Beta focuses on short-term price movements, potentially overlooking long-term investment fundamentals.
4. Market Index Dependence: Its effectiveness varies with the chosen market index, which can lead to inconsistent risk assessments.
5. Unsystematic Risk Overlook: Beta measures only systematic risk, ignoring specific risks tied to individual companies or sectors.
6. Sector Bias: Some sectors inherently have higher or lower betas, which might not accurately reflect actual risk levels.
7. Leverage Effects Ignored: Beta does not distinguish between risks from operational activities and those due to financial leverage.
8. Limitations with Illiquid/Small Stocks: It is less reliable for illiquid or small-cap stocks, where price movements can be exaggerated.
9. Ignoring Fundamental Changes: Beta does not account for shifts in a company’s fundamentals, such as changes in management or strategy.
10. Linear Assumption: It assumes a linear relationship between stock and market returns, simplifying complex market dynamics.

Beta is best utilized as a measure of a stock's volatility relative to the overall market, rather than a direct measure of risk. This makes it particularly useful for investors interested in understanding how a stock might react relative to market movements. It is most effective when applied to large-cap, highly liquid stocks in sectors with stable market conditions, where historical trends offer a reliable gauge of future volatility. Investors can leverage beta for portfolio diversification, using it to balance assets with varying degrees of market responsiveness.

However, it's important for investors to view beta as a component of risk assessment, supplementing it with other analytical tools and qualitative evaluations to build a well-rounded understanding of potential investments.

The Bottom Line

Beta, as a primary measure of systematic risk, equips investors with the ability to assess a stock's volatility in relation to the overall market. Calculating stock and portfolio beta in Excel, a skill that enables precise evaluation of market-relative volatility, is a key aspect of applying this understanding effectively.

Building on this foundation, the distinction between levered and unlevered beta further refines risk analysis. Levered beta accounts for the impact of a company's debt, offering a view of both business and financial risk. In contrast, unlevered beta focuses exclusively on business risk, thereby excluding the influence of financial leverage. This differentiation is essential for a nuanced understanding of a company's true risk profile.

While beta is invaluable for evaluating systematic risk, it should not be the only measure used in risk assessment. Pairing beta with other financial analyses and qualitative evaluations creates a more comprehensive and balanced approach. This combination ensures a deeper and more accurate understanding of investment risks and opportunities, thereby enhancing the quality of investment decisions.