In this article, I will show you how to calculate and interpret the Arbitrage Pricing Theory (APT). Developed by economist Stephen Ross in 1976, the APT presents a multifactorial approach to asset pricing, which extends beyond the Capital Asset Pricing Model (CAPM). The CAPM is a fundamental model in finance that attempts to explain the relationship between the expected return on a stock investment and market risk. While not a strict prerequisite for understanding the APT, knowledge of the CAPM can provide a useful foundation, as both describe the equilibrium expected return for assets.

Unlike CAPM, which identifies market risk as the sole factor affecting the returns of a portfolio (covariance with the market portfolio (beta (β)), APT recognizes multiple risk factors (e.g., inflation, interest rates, GDP, etc.) that could influence the performance of financial assets. The multifactor structure of APT adds complexity compared to CAPM but, in theory, provides a more precise method for calculating a company's discount rate.

This article therefore delves into the intricacies of APT, providing a comprehensive understanding of its formulation, application, and implications in the financial world.

Core Concepts and Assumptions of the Arbitrage Pricing Theory (APT)

The Arbitrage Pricing Theory (APT) is founded on the law of one price, which claims that assets with identical risk and return profiles should command equivalent prices. Any deviations from this equilibrium suggest arbitrage opportunities that allow investors to buy undervalued assets and sell overvalued ones for a risk-free profit.

Consider the basic example of two portfolios, X and Y, which have the same level of systematic risk, as indicated by their betas of 1.5. Despite this, they offer different expected returns, presenting an arbitrage opportunity as illustrated in the table below:

Arbitrage Pricing Theory (APT) Arbitrage Example

In this scenario, the investor capitalizes on the price difference by short selling Portfolio Y to finance the purchase of Portfolio X, yielding a risk-free profit of $50 per $1,000 invested. The profit is considered risk-free because the equal but opposite betas indicate that market risk is offset.

Market forces are expected to naturally correct this mispricing. As investors move toward the undervalued Portfolio X, its price should rise. Conversely, the price of the overvalued Portfolio Y is likely to decrease as more investors engage in short selling. This process will continue until the expected returns of both portfolios align with their risk levels, exemplifying the APT's self-correcting mechanism and the law of one price.

To understand the APT further, we can examine the APT line chart, which depicts the relationship between expected returns and systematic risk exposure. This line is similar to the Security Market Line (SML) from CAPM. However, the APT allows for multiple risk factors, while the SML considers only the market portfolio's risk:

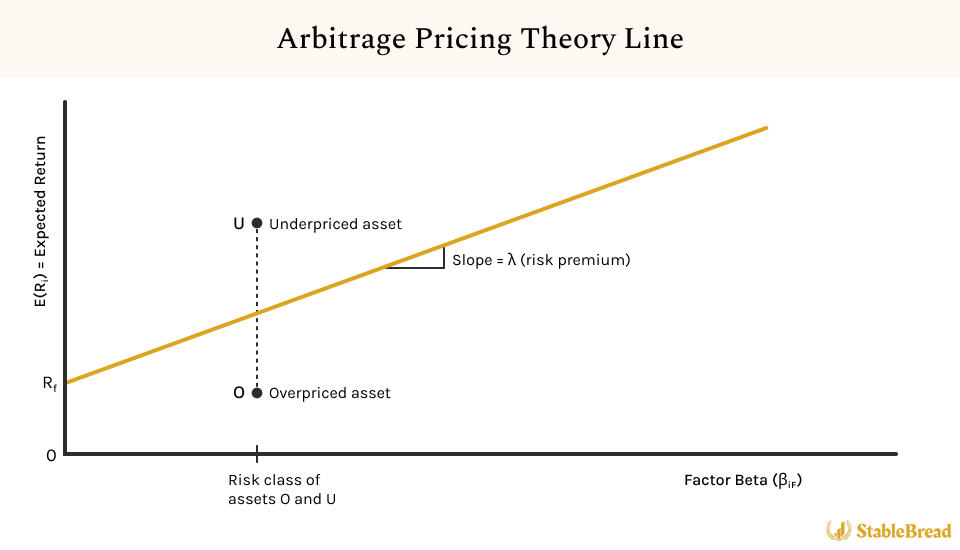
The formula depicted below outlines the APT line, as shown in the illustration above. While this single-factor model is simplified for educational purposes, it's important to note that the APT usually incorporates a more diverse array of factors to determine expected returns, which we will explore in greater detail further on.

E(R_i​) = R_f​ + β_iF ​* (E(F) - R_f)

where:

• E(R_i) = expected return on asset i
• R_f​ = risk-free rate
• β_iF = sensitivity of investment i to the factor F
• E(F) - R_f = risk premium, or lambda (λ)

This line indicates the positions of assets U (underpriced) and O (overpriced) which deviate from the law of one price. Even though assets U and O fall within the same risk category, they have differing expected returns.

The chart points out assets U and O as anomalies, highlighting the discrepancy between their expected returns and risk levels. Rational investors are expected to sell asset O (because it's overpriced) and purchase asset U (because its rate of return is unusually high), thereby exploiting these irregularities. This should lead to an adjustment in prices and support the market equilibrium as anticipated by the APT model.

Following the concepts of arbitrage and the law of one price, it's important to consider the foundational assumptions that enable the APT to function in the financial markets. The APT's effectiveness in pinpointing mispricings hinges on these core assumptions:

• Multiple Systematic Factors: The theory recognizes that an asset's returns can be influenced by various economic factors, not just overall market risk. This aligns with the APT model's consideration of multiple risk factors rather than the single factor in CAPM.
• No Arbitrage: APT is predicated on the idea that any arbitrage opportunity – buying undervalued assets and selling overvalued ones – is quickly acted upon by traders, which ensures prices are fair and reflective of all known risks.
• Diversifiable Specific Risks: According to APT, individual asset risks that are not systemic can be mitigated through diversification, effectively neutralizing their impact on a well-balanced portfolio.

The principles that form the basis of the APT framework also assume:

• Risk-Averse Investors: It's assumed that investors will naturally avoid risk where possible, preferring investments that offer the most return for the least risk.
• Efficient Markets: In keeping with APT's assumptions, markets are considered efficient, instantaneously incorporating all available information into asset prices.
• Perfect Capital Markets: APT presupposes ideal market conditions, such as the absence of taxes, transaction costs, and other imperfections that could impede trading.
• Infinite Assets: The theory assumes a broad and deep market with an infinite number of assets, allowing for the creation of perfectly diversified portfolios that can eliminate unsystematic risk.

The APT's flexibility in accounting for multiple risk factors and its lack of reliance on normally distributed returns or a singular market portfolio gives it an edge over CAPM. It is versatile, applicable across different investment horizons, and allows for unrestricted short-selling – an essential component of arbitrage strategies. While APT and CAPM both assume risk-averse behavior in efficient markets, APT's wider scope of assumptions offers a more dynamic approach for understanding risk and return in financial markets.

Arbitrage Pricing Theory (APT) Formula

The Arbitrage Pricing Theory (APT) claims that the expected return on an asset is a linear function of various macroeconomic risk factors, with the asset's sensitivity to each factor represented by factor betas.

The APT formula can accommodate multiple macroeconomic factors and their respective betas, allowing for a more comprehensive analysis of expected returns. This is shown in the formula below:

E(R_i) = R_f + β_i1*[E(F₁) - R_f] + β_i2*[E(F₂) - R_f] + β_i3*[E(F₃) - R_f] + ... + β_iK*[E(F_k) - R_f] + ε_i​

where:

• E(R_i) = expected return on asset i
• R_f = risk-free rate
• β_ik = sensitivity of the asset's return to factor k
• E(F_k) = expected return due to factor k
• ε_i = firm-specific or idiosyncratic risk unexplained by macro factors (often omitted in the APT formula)

With the APT formula, the expected rate of return is composed of the risk-free rate plus the product of each risk factor's premium and the asset's beta with respect to that factor. This approach allows for a nuanced calculation of expected returns, accounting for various systematic risks.

To elaborate further, β_iK*[E(F_k) - R_f] quantifies the risk premium (aka lambda (λ)) associated with factor k, reflecting the extra expected return for taking on that specific factor's risk. This is done by subtracting the risk-free rate (Rf) from the expected return of the factor E(F_k) to isolate the premium.

The term "factor" in APT refers to any variable that systematically influences the expected return of an asset. The beta (β) of an asset measures its sensitivity to these factors. Put simply, beta greater than 1 means the asset is more volatile than the market, while less than 1 means it's less volatile. Factor betas can be computed through regression analysis, which shows how much the expected return of an asset changes with each unit change in a systematic factor.

Lastly, the term ε_i represents the unique, non-systematic returns specific to an individual asset. While the APT assumes these risks can be minimized through diversification in a large portfolio, they are shown in the APT formula above to acknowledge any undiversified risk that may persist.

How to Implement the Arbitrage Pricing Theory (APT)

The Arbitrage Pricing Theory (APT) provides a framework for assessing asset returns by considering various risk factors and their impact on expected returns. Implementing APT involves establishing a risk-free rate and then identifying pertinent risk factors that influence asset prices, as discussed further below.

Risk-Free Rate (R_f)

In the APT model, the risk-free rate is the theoretical return of an investment considered to be free of risk, serving as a benchmark for the minimum return investors should expect. This rate is foundational for gauging the additional returns required from riskier investments.

The selection of an appropriate risk-free rate within the APT framework is contingent on the time horizon of the assets being analyzed. The three-month T-bill rate is commonly used for short-term analysis due to its immediate reflection of current market conditions. In contrast, for long-term investment considerations, yields on longer-dated government securities, such as the 10-year or 20-year Treasury bonds, are often more appropriate. These longer-term rates better match the investment's time frame and provide a reflection of the long-term expectations for risk-free returns.

Treasury securities are considered risk-free assets because they are backed by the full faith and credit of the U.S. government, which has the authority to levy taxes and print currency. This backing effectively eliminates the risk of default, making these securities the safest investment from a credit standpoint. As a result, they are used as the benchmark for the risk-free rate in financial models, including the APT.

The live chart below, for reference, compares the yields of the 3-month and 10-year Treasury yields:

By incorporating the risk-free rate, the APT model acknowledges that even in the absence of systemic risk factors, investors should at least achieve a return equivalent to that of a risk-free asset. This rate is critical in calculating the expected return of an asset when applying the APT, as it serves as the starting point to which risk premiums associated with various factors are added.

APT Risk Factors

The Arbitrage Pricing Theory (APT) suggests that a variety of risk factors are important in determining the returns on assets. While Stephen Ross (the founder of the APT) did not specify the factors that should be used in this model, others have introduced different macroeconomic, industry-specific, and company-specific factors that claim to explain stock market returns.

Thus, selecting factors for the model should be grounded in empirical research and guided by the investor's judgment, with the general consensus being that four or five factors are sufficient to account for the majority of a security's return.

The risk factors commonly recognized for their statistically significant explanatory power include:

• Macro-Economic Risk Factors: These encompass broad economic forces that can influence all investments. For example, unexpected changes in inflation rates can change the value of future cash flows, and fluctuations in interest rates can affect everything from corporate profits to consumer spending. Alterations in the money supply may reflect shifts in economic policy that could sway market performance, and variations in GDP growth rates are indicators of overall economic health.
• Industry Risk Factors: These factors are specific to industry sectors and include the level of competition, which can influence market dominance and profit margins, and industry growth rates, which affect the potential for growth and profitability within a sector.
• Company-Specific Risk Factors: Pertaining to individual companies, these factors include corporate debt levels, which speak to a company's financial health; the size of the company, with larger firms typically having greater resources; and efficiency metrics like return on assets, which assess a company's ability to generate profits from its asset base.

Further, empirical research has often aimed to identify significant factors that explain the returns of a broad set of assets.

To begin, in "An Empirical Investigation of the Arbitrage Pricing Theory," published in 1980, Roll and Ross delved into the intricacies of stock returns by examining data spanning from 1962 to 1972. Their research corroborated the APT as a robust alternative to the CAPM. They discovered that stock returns are shaped by a complex interplay of multiple factors. While they determined the existence of three to four influential priced factors within the returns generation process, the exact nature of these factors remained unspecified. Roll and Ross’s findings also demonstrated a direct relationship between expected returns and securities' factor loadings, discounting the role of an individual security’s variance in explaining returns, thus casting doubt on the traditional single-factor approach of CAPM.

After Roll and Ross laid the groundwork for the APT in their 1980 study, Chen, Roll, and Ross’s 1986 paper "Economic Forces and the Stock Market" advanced this theory by thoroughly examining specific macroeconomic variables. While their initial research suggested that multiple factors were at play in influencing stock returns, it was the subsequent study that clarified this by pinpointing four key systematic economic risks. These risks are discerned as being integral to the pricing of assets in the market:

1. Unanticipated Inflation: This factor measures the impact on stock returns when actual inflation rates diverge from what was expected by the market.
2. Industrial Production: An indicator of economic activity, particularly within the industrial sector, that can signal shifts in cash flow expectations for companies.
3. Yield Spread Between High-Grade and Low-Grade Corporate Bonds: This spread is an indicator of investor risk preferences, reflecting the perceived risk of default and the overall confidence in the corporate bond market.
4. Difference in Term Structure of Interest Rates: Shifts between short- and long-term interest rates that were not anticipated by the market, which can influence economic forecasts and valuation models.

Separately, they also consider:

• Expected Inflation: Recognized in the model but deemed less impactful, as it represents inflation expectations that are already factored into prices by the market.

The 1986 research by Chen, Roll, and Ross confirms that these variables systematically influence stock market returns and carry risk premiums, meaning they are priced by the market. This evidence not only supports the validity of APT but also expands its scope by identifying specific factors that drive asset pricing, thereby providing a more detailed lens through which to view market dynamics than what CAPM offers.

Building on the findings of Chen, Roll, and Ross's 1986 research, which confirmed the influence of specific macroeconomic variables on stock market returns, the Salomon Smith Barney Factor Model utilizes a multi-factor arbitrage pricing model to extend the breadth of risk factors considered in asset pricing.

This multi-factor model adds to the APT framework by including a diverse set of factors that further explain the behavior of asset prices in the market. The components of the Salomon Smith Barney Factor Model include:

• Market's Trend or Drift: Reflecting the persistent direction or momentum that is observed in the stock market over time.
• Economic Growth: Representing the effects of macroeconomic growth or contraction, this factor puts forward that the general economic climate is a significant driver of market performance.
• Credit Quality: This element examines the impact of changes in the creditworthiness of debt issuers and the overall credit conditions, which can lead to immediate adjustments in asset values.
• Interest Rates: Acknowledging the direct influence of both short-term and long-term interest rates, which affect the cost of capital and are indicative of monetary policy shifts and economic forecasts.
• Inflation Shock: Instead of general inflation levels, this factor specifically targets sudden and unanticipated inflation changes that catch the market off-guard.
• Small-cap Premiums: Incorporating the empirical finding that smaller-cap companies often outperform larger ones, this factor compensates for the additional risk that such stocks carry.

In short, the Salomon Smith Barney Factor Model provides a nuanced perspective on the dynamics that drive market performance, complementing the principles of the APT. It also introduces additional factors for investors' consideration, which extend beyond the scope of Chen, Roll, and Ross' research, potentially offering a more granular approach to understanding asset prices.

In essence, the empirical research and models discussed above establish a guiding framework for identifying and selecting the most appropriate factors for APT calculations. These evidence-based insights can be useful for investors seeking to refine their approach to asset valuation and risk assessment within the APT framework.

International Arbitrage Pricing Theory (IAPT)

The International Arbitrage Pricing Theory (IAPT) extends the traditional Arbitrage Pricing Theory (APT) by integrating exchange rate risks, a critical factor in today’s interconnected financial markets. In his 1983 study, "International Arbitrage Pricing Theory," Bruno Solnik modified the APT to factor in the volatility of international exchange rates, thus enhancing the model's global applicability.

The significance of considering various risk factors in asset pricing was echoed by Fama and French in their 1992 three-factor model, as presented in "The Cross-Section of Expected Stock Returns." Their research implied that a set of core factors, such as market risk, company size, and book-to-market value, might be universally relevant, affirming Solnik’s hypothesis about international market dynamics.

• Related: How to Calculate and Interpret the Fama and French and Carhart Multifactor Models

Further examination of these concepts can be found in the 2012 study "Empirical Investigation of the International Arbitrage Pricing Theory." This study empirically evaluated the IAPT model, emphasizing how shifts in base currency influence asset risk premiums on a global scale. Researchers dissected investor returns by isolating currency effects and other global factors, applying the Fama and French three-factor model to measure the currency’s impact. The findings of this study corroborated the IAPT's premise, reinforcing its role in capturing the complexities of pricing international assets and underscoring the significance of exchange rate risks in global asset valuation.

APT Example

To effectively apply the Arbitrage Pricing Theory (APT), we can utilize the macro-economic factors that Chen, Roll, and Ross identified as significant in explaining security returns. These factors include unexpected changes in inflation rates, GNP as indicated by an industrial production index, investor confidence as reflected in the default premium on corporate bonds, and shifts in the yield curve.

For a practical example, consider an asset with the following sensitivities (betas) to the identified macro-economic factors and the current unexpected changes (surprises) in these factors:

1. Beta to Inflation Surprise (β1): 0.5, Inflation Surprise (F1): 1%
2. Beta to GNP Surprise (β2): 1.2, GNP Surprise (F2): 3%
3. Beta to Default Premium Surprise (β3): -0.7, Default Premium Surprise (F3): -0.5%
4. Beta to Yield Curve Surprise (β4): 0.3, Yield Curve Surprise (F4): 0.2%

If the current risk-free rate (R_f) is 2%, the expected return (ER) for the asset can be calculated using the APT formula:

E(R) = 2% + (0.5 * 1%) + (1.2 * 3%) + (-0.7 × -0.5%) + (0.3 * 0.2%) --> 6.51%

This expected return of 6.51% reflects the asset's sensitivity to the systematic risks of the market, incorporating the foundational risk-free rate. In real-world applications, investors might substitute macro-economic data with more readily available market indices or prices from spot or futures markets. Suitable proxies for these macro-economic factors could include short-term interest rates, the spread between long-term and short-term interest rates, broad market indices like the S&P 500 or NYSE Composite, and prices of commodities such as oil or precious metals.

By incorporating these factors into the APT framework, investors can estimate an asset's expected return, taking into account the systematic risks of the market. This method facilitates the creation of diversified portfolios that strategically balance risk and return, aligning with the insights provided by the studies previously discussed.

Calculating Beta Values and Risk Premiums in APT Applications

To highlight the relationship between risk factors and individual assets, as mentioned in the prior section, we focus on assessing beta values. This involves an in-depth analysis using a vast array of historical data. By implementing mathematical regression, either through sophisticated algorithms or manually inputted data, these beta coefficients are derived. These coefficients are indicative of how sensitive the returns of an asset are to each identified risk factor.

When extending APT to encompass a portfolio with a variety of assets, the process requires a separate regression for each asset against its associated factors. Resolving these equations yields the individual risk premiums, which are instrumental in formulating expected returns for the portfolio based on the systematic risks each asset is exposed to.

How to Calculate the Arbitrage Pricing Theory (APT) in Excel

Calculating the Arbitrage Pricing Theory (APT) model in Excel requires a step-by-step process involving the collection of relevant data, setting up the model, performing regression analysis, and finally calculating the expected returns for the assets. Below are the detailed steps you would follow:

Step #1: Data Collection

1. Identify the Risk Factors: Decide on the macroeconomic and industry-specific factors you wish to include in your APT model (e.g., inflation rate, GDP growth, interest rates).
2. Gather Historical Data: Collect historical data for the risk factors and the returns of the assets you are analyzing over the same time period.
3. Risk-Free Rate: Obtain the historical risk-free rate (e.g., the yield on a 10-year Treasury bill).

Step #2: Setup in Excel

4. Input Data: Enter the historical data for the asset returns, risk-free rates, and risk factors into separate columns in Excel.
5. Calculate Excess Returns: Create a new column to calculate the excess return for each asset, which is the asset’s return minus the risk-free rate for the same period.

Step #3: Regression Analysis

6. Run Regression: Use the Data Analysis ToolPak in Excel (which must be activated) to perform a regression analysis. Set the excess returns of the asset as the dependent variable (Y range) and the risk factors as the independent variables (X range).
7. Interpret Results: Once the regression is completed, Excel will provide you with the beta coefficients for each risk factor, which represents the sensitivity of the asset’s returns to that factor.

Step #4: Calculate Expected Returns

8. Current Factor Values: Input the current or expected values of each of the risk factors in a new row.
9. Risk Premiums: Multiply each factor’s beta coefficient by its current or expected value to determine the risk premium for each factor.
10. Sum of Risk Premiums: Calculate the sum of all the individual risk premiums.
11. Expected Return Formula: Add the current risk-free rate to the sum of the risk premiums to find the expected return on the asset according to the APT model.

Step #5: Analysis

12. Analyze and Compare: Compare the calculated expected returns to the actual returns or the expected returns of other assets to make investment decisions. Based on your analysis, you may need to adjust the factors you’ve included or the time period of your data, and then repeat the regression analysis.

Keep in mind that this is a simplified overview of the process. In practice, APT calculations can become quite complex, especially when dealing with large datasets and multiple assets. Additionally, you should ensure the factors you choose are relevant and that the data is of high quality to produce reliable results.

Pros and Cons of the Arbitrage Pricing Theory (APT)

While APT offers a more nuanced view of risk and return than CAPM, it's not without its limitations. This section will explore the advantages and disadvantages of using APT in investment analysis and portfolio management.

Pros of the APT

• Comprehensive Risk Diversification: The APT incorporates a variety of market risk factors, enhancing risk assessment and diversification.
• Adaptability: Investors have the flexibility to modify the model to reflect factors that are pertinent to their investment contexts.
• Relaxed Assumptions: In contrast to the CAPM, APT does not hinge on the efficiency of the market portfolio.
• Empirical Validation: Research, such as Chen's 1983 study, demonstrates a strong positive correlation between APT factors and the market portfolio, affirming the model's capacity to explain variations in returns with multiple risk factors. This suggests APT's superiority in predicting average returns over the Security Market Line (SML), and its ability to account for variances that SML cannot.

The APT is notable for its flexibility in incorporating various risk factors, for its reliance on a simpler set of assumptions compared to other models (like the CAPM), and for aligning with the SML in scenarios where only a single risk factor is analyzed.

Cons of the APT

• Factor Specification: The APT falls short in providing definitive instructions for choosing risk factors, resulting in potential uncertainty during its application. In contrast, the Fama-French models present a multifactor alternative with a clearly defined set of three to five factors that account for market returns.
• Estimation Challenges: Determining factor betas with precision is difficult, and the APT's results are sensitive to these calculations.
• Limited Empirical Support: The APT does not have as extensive empirical validation as CAPM, leading to less confidence in its practical implementation.
• Unrealistic Arbitrage Assumption: APT assumes arbitrageurs can use all proceeds from short sales to fund long positions, which is not typically feasible for most market participants.

Although the APT offers a more intricate framework than CAPM by considering multiple risk factors, it grapples with practical difficulties such as the absence of explicit factor guidance, complex estimation requirements, and assumptions about arbitrage that may not hold true in real-world scenarios.

The Bottom Line

The Arbitrage Pricing Theory (APT) refines asset pricing by incorporating multiple risk factors, providing a layered approach superior to CAPM's singular focus. It assumes a market equilibrium maintained by the law of one price, thus negating arbitrage opportunities. This multifaceted model weighs diverse economic indicators, market behaviors, and investor preferences to forecast asset returns. While APT's flexibility is advantageous, allowing for a tailored analysis inclusive of various macro and microeconomic factors, it also demands a complex estimation process.

In application, APT goes beyond the abstract, requiring careful selection of risk factors and detailed regression analysis to ascertain assets' risk sensitivities. Despite its comprehensive approach and empirical support from studies such as Chen's 1983 work, APT faces critiques for its ambiguous factor selection and the practicality of its assumptions, especially in relation to the more concrete factor definitions offered in other models, such as the Fama-French multifactor models.

For value investors, APT's methodology is particularly relevant. It judges an asset's mispricing by comparing its current price to its calculated value based on future cash flows, discounted by a rate reflective of its risk exposure to various economic elements. This process allows investors to gauge an asset's intrinsic value, providing a strategic edge in identifying undervalued investments or selling those at a premium.