In this article, I will demonstrate how to use the Three-Stage Dividend Discount Model (DDM) to value dividend-paying stocks. As the most advanced among the dividend discount valuation methodologies, this model introduces an initial phase of extraordinary growth, followed by a period where the growth rate either linearly declines or increases, before finally transitioning into a phase of stable growth extending into perpetuity. This progression mirrors the typical lifecycle of a maturing business, allowing the Three-Stage DDM to address many of the limitations found in simpler models. When applied correctly, it can be the most accurate DDM method for capturing a stock's true value, owing to its nuanced consideration of different growth stages and dividend payout ratios.

This article will detail the model's formula, examine its key assumptions, and identify situations where it proves particularly useful. Additionally, we'll address the limitations of the Three-Stage DDM in stock valuation and conclude with a detailed real-life example to illustrate its practical application in valuing dividend-paying stocks.

Three-Stage Dividend Discount Model Explanation

The Three-Stage Dividend Discount Model (DDM) represents an evolution in the approach to valuing dividend-paying stocks, combining elements from the Two-Stage DDM and the H-Model. It's designed to offer a more comprehensive assessment of a company's dividend growth over time by segmenting the growth trajectory into three distinct phases.

The illustration below captures the expected dividend growth over time in the Three-Stage DDM:

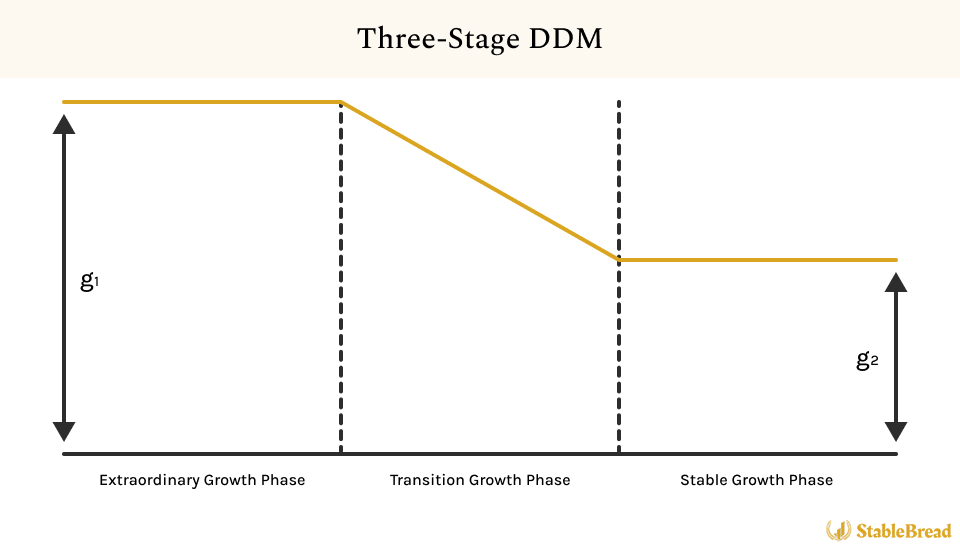
As you can see, the Three-Stage DDM captures a company's dividend growth in three phases. Initially, there's a high growth phase, often marked by aggressive expansion or innovation. This is followed by a linearly declining growth phase, where dividend increases slow as the company stabilizes and matures. The final phase is stable growth, characterized by steady and predictable dividend increases, reflecting the company's established market position. This model adeptly mirrors varied growth scenarios across a company's lifecycle.

The dividend payout ratio is also assumed to vary across different phases. Initially, in the high growth phase, companies often retain a larger portion of their earnings to reinvest in growth opportunities, leading to a lower dividend payout ratio. As growth slows in the transitional phase, companies typically begin to increase their dividend payout ratio, indicating a reduced need for reinvestment. In the final stable growth phase, companies generally have a high payout ratio, as they are more likely to distribute a larger portion of their earnings to shareholders, reflecting limited reinvestment opportunities and established market positions.

While the Three-Stage DDM typically begins with a high-growth phase, it's adaptable enough to accommodate scenarios where a company initially faces low or negative growth due to market challenges or heavy investments in research and development. In such situations, this initial phase of subdued growth may be followed by a period of rapid expansion, eventually leading to a stable growth phase. Correspondingly, the pattern of dividend payout ratios across these stages would be adjusted to align with this reversed growth trajectory.

In essence, the Three-Stage DDM's complexity and versatility make it a powerful tool for estimating a stock's intrinsic value. It accounts for the nuances and fluctuations in dividend growth rates, unlike models that assume a fixed growth rate indefinitely. While precise, it's important to remember that a stock's market price is influenced by a variety of factors, not just its dividend valuation. Therefore, the Three-Stage DDM is best used as an indicator of a stock's potential over or undervaluation, assisting investors in identifying profitable long-term investment opportunities.

Three-Stage Dividend Discount Model Formulas

The Three-Stage Dividend Discount Model (DDM) is the most intricate version of the dividend discount models, synthesizing elements of the Two-Stage DDM and the H-Model, as mentioned prior. It's built on the premise that a stock's value can be calculated by determining the present value of expected dividends during the initial extraordinary growth phase, the subsequent transitional phase, and the projected terminal value at the onset of the stable growth phase.

There are two formulas that investors can utilize to calculate the Three-Stage DDM and determine a stock's value. The first is a more direct approach, focusing solely on the present value of expected dividends, and is suitable for broad analysis. The second formula is more detailed, factoring in variations in earnings and dividend payouts to estimate dividends. It also incorporates discount rates across all three phases, thereby offering a view more grounded in the assumptions of the Three-Stage DDM.

The choice between these formulas hinges on the depth of analysis required. The first is preferred for its simplicity and broad applicability, while the second, catering to companies likely to experience notable shifts in earnings, payout ratios, and/or risk profiles, offers more detailed insights. Both are tailored to reflect a company's changing growth phases and dividend patterns.

Three-Stage DDM Formula: Option #1

The first Three-Stage DDM formula offers a more direct approach, as it does not factor in expectations of return on equity (ROE) and dividend payout ratio (DPR), and keeps the discount rate (r_e) constant. Despite this straightforward framework, it still involves a comprehensive calculation process.

The first Three-Stage DDM formula is shown below:

where:

• P₀ = stock's fair value (at year 0)
• DPS₀ = annual dividends per share (at year 0)
• DPS_n = expected dividend at the end of the extraordinary growth phase
• n = final year of first-stage dividend growth (i.e., when dividend growth rate changes from g₁ to g₂)
• H = one-half the duration of the transitional period
• g₁ = extraordinary high/low dividend growth rate (first stage)
• g₂ = perpetual dividend growth rate (third/final stage)
• r_e = discount rate (aka required rate of return)

To effectively navigate the simplified Three-Stage DDM formula, it's helpful to dissect the formula into its three stages:

1. First Phase (Extraordinary Growth Phase): Begin with the current dividend (DPS₀) and forecast its growth at an extraordinary growth rate (g₁) annually until this phase concludes (n years). To determine the present value of each year's dividend, DPS₀ is grown by g₁ for that specific year and then discounted to its present value using the discount rate (r_e), commonly derived using the Capital Asset Pricing Model (CAPM).
2. Transition Phase: This phase accounts for the gradual shift from the extraordinary growth rate (g₁)​ to the stable growth rate (g₂)​. The transitional value, calculated using the term "DPS_n​ * (1 + g_2​) + DPS_n​ * H * (g₁​ - g₂​)," is then discounted back to present value using the rate "r_e." Here, "H" adjusts the transition phase, representing one-half the duration of the transitional period.
3. Final Phase (Stable Growth Phase): The final stage assumes the company's dividends grow at a constant rate g₂​ into perpetuity, which is a premise of the Gordon Growth Model (GGM). This terminal value is calculated once and then discounted back to present value using the same discount rate "r_e," representing the assumption of a mature company in a stable market environment.

In closing, the stock's current fair value (P₀), is derived by aggregating the present values from each growth phase. Accurate estimation of the initial extraordinary growth rate (g₁), the stable growth rate (g₂), the discount rate (r_e), and the half-life of the transition period (H) is crucial. This approach ensures that the model accurately captures the company's financial trajectory through its high growth, transition, and stable phases, leading to a refined stock valuation.

Three-Stage DDM Formula: Option #2

The second Three-Stage DDM formula adopts a nuanced approach, considering the earnings per share (EPS) and the dividend payout ratio (DPR) across different phases. It accounts for distinct payout ratios during the extraordinary-growth, transitional, and stable growth phases, reflecting the anticipated shifts in the proportion of earnings paid out as dividends in each phase. This method proves useful when the company's DPR is expected to undergo significant changes through its growth stages. Additionally, this formula employs three distinct discount rates (r_e,1, r_e,2, and r_e,3) for each phase, aligning more closely with the evolving risk profile of a company as it progresses through these stages.

The second Three-Stage DDM formula is shown below:

where:

• P₀ = stock's fair value (at year 0)
• DPS_t = annual dividends per share (in year t)
• EPS_t = earnings per share (in year t)
• DPR₁ = dividend payout ratio in extraordinary growth phase
• DPR₂ = dividend payout ratio in stable growth phase
• n₁ = final year of the extraordinary growth phase where the dividend growth rate is g₁
• n₂ = year when the stable growth rate g₂ takes effect after the transition phase
• g₁ = extraordinary high/low dividend growth rate (first stage)
• g₂ = perpetual dividend growth rate (third/final stage)
• r_e,1 = discount rate (aka required rate of return) in extraordinary growth phase
• r_e,2 = discount rate (aka required rate of return) in transition phase
• r_e,3 = discount rate (aka required rate of return) in stable growth phase

To apply the more complex Three-Stage DDM formula, let's break down the valuation process into the corresponding growth phases:

1. First Phase (Extraordinary Growth Phase): In this phase, calculate the present value of dividends that are projected based on the earnings per share (EPS) for each year during the extraordinary growth phase. These earnings are expected to grow at an extraordinary rate (g₁) and are adjusted by the dividend payout ratio (DPR₁) specific to this phase. Each expected dividend is then discounted to its present value using the discount rate (r_e,1), which reflects the risk and potential returns during this initial growth phase.
2. Transition Phase: This phase involves accounting for the dividends per share (DPS) during the period following the extraordinary growth phase but before the stable growth phase. These dividends are discounted to present value using the discount rate (r_e,2) appropriate for the transition phase. Given a high initial growth rate, this phase would be characterized by a linear deceleration in growth as the company transitions toward a more stable and mature state.
3. Final Phase (Stable Growth Phase): In the final stage, the terminal value of the company is estimated. This value is based on the last EPS before entering the stable phase (EPS_n2), which is projected to grow at a constant and stable rate (g₂), and is then adjusted by the dividend payout ratio (DPR₂) expected to prevail during this mature phase. The resulting terminal value, which assumes a perpetual growth of dividends (g₂), is then discounted to present value using the discount rate (r_e,3), the initial discount rate (r_e,1), and all of the calculated discount rates in the transition phase (r_e,2).

In closing, each phase is summed to determine P₀, the stock's fair value at the current time (year 0). The model requires careful estimation of the growth rates (g₁ and g₂), payout ratios (DPR₁ and DPR₂), and discount rates (r_e,1, r_e,2, and r_e,3) in each phase, along with the lengths of the extraordinary growth (n₁) and transition phases (n₂). This comprehensive approach aims to capture the changing dynamics in a company's growth trajectory and provide an accurate stock valuation.

Assumptions of the Three-Stage Dividend Discount Model

The Three-Stage Dividend Discount Model (DDM) is based on a set of core assumptions essential for evaluating companies through different growth phases:

• Initial Extraordinary Growth Phase With Defined Duration: The model begins with the firm experiencing an extraordinary growth phase, characterized by high, low, or negative growth rates due to various factors such as expansion, innovation, or restructuring. The duration of this phase is crucial and must be clearly defined, as it significantly impacts the subsequent valuation stages.
• Linear Transition to Stable Growth: The model assumes a gradual decrease in both growth rates and discount rates, paired with a corresponding increase in the dividend payout ratio, as the company transitions from high growth to stability. This trend reflects the diminishing risk and decreasing reinvestment needs of a maturing company. It's important to note that if the initial extraordinary growth phase features low or negative dividend growth rates, this linear growth transition relationship would be inverted.
• Correlation Between Dividend Payout Ratio and Growth Rate: The model posits a variable relationship between the dividend payout ratio and growth rates. In high growth phases, lower payout ratios are common due to reinvestment strategies. In contrast, during low or negative growth periods, higher payout ratios might prevail due to limited reinvestment opportunities. As stability approaches, the payout ratio generally increases, reflecting a shift to lower reinvestment needs and greater profit distribution.
• Risk Profile, Cost of Capital, and Financial Policy Adjustments: As the firm progresses through its growth stages, adjustments to its risk profile, cost of capital, and financial policies are anticipated. This includes changes in the cost of equity, which is typically higher during the risky high-growth phase but decreases as the company stabilizes. Additionally, consistency in financial and operational policies is assumed across different growth phases, since significant changes can affect both growth rates and payout ratios.

These assumptions are essential for applying the Three-Stage DDM to firms with varied growth trajectories. Understanding these assumptions is key to accurate valuation, though their relevance may differ based on the company's unique circumstances.

Relevant Applications of the Three-Stage Dividend Discount Model

The Three-Stage Dividend Discount Model (DDM) is highly effective for evaluating companies across various growth stages and dividend payout scenarios, as detailed below:

• Dividend Alignment and Initial Extraordinary Growth: The Three-Stage DDM is ideal for firms whose dividend payouts are closely aligned with their free cash flow to equity (FCFE), defined as the cash available for distribution to shareholders after accounting for capital expenditures and debt payments, and who are in a phase of extraordinary growth. This period, characterized by rapid expansion due to unique competitive advantages or market opportunities, is expected to have a defined duration.
• Gradual Growth Rate Decline and Stable Leverage: The model adeptly captures the gradual reduction in growth rates as firms mature, maintaining stable leverage to signify consistent financial and capital strategies throughout their lifecycle. This consistency in leverage ensures a predictable risk assessment, vital for accurate valuation, while the smooth transition in growth rates realistically reflects the typical progression of firm development.
• Adaptability to Payout and Risk Profile Shifts: The model is highly adaptable to companies expecting changes in dividend payout policies and risk profiles, aligning with the varied financial strategies across different growth stages. This adaptability makes it ideal for rapidly growing firms, which often adjust dividend policies in response to changing market dynamics and internal financial considerations. As these firms move from aggressive expansion to more sustainable growth, the model adeptly captures the evolving risk profiles and the consequent adjustments in dividend strategies, offering a comprehensive view of their financial evolution.
• Realistic Business Lifecycle Representation: The model effectively reflects real-world business cycles. It's particularly suitable for companies that initially experience high growth, often driven by innovation or market dominance. As these companies mature, they transition to more stable growth, influenced by increased competition and market saturation. This model provides a nuanced understanding of the evolving growth dynamics and competitive pressures throughout a company's lifecycle.

In summary, the Three-Stage DDM stands out for its ability to adapt to various growth scenarios, its relevance to companies with changing dividend policies, and its flexibility in adjusting to shifts in risk profiles and capital structures. Its structured approach, mirroring realistic business cycles and market dynamics, makes it a comprehensive and versatile tool for accurate stock valuation, particularly for firms undergoing significant growth transitions.

Limitations of the Three-Stage Dividend Discount Model

While the Three-Stage Dividend Discount Model (DDM) provides a comprehensive framework for stock valuation, particularly for companies with dynamic growth, earnings, and payout ratio patterns, it's essential to understand its limitations. These limitations are especially pronounced in varied market conditions:

• Complexity and Sensitivity in Estimating Inputs: The model requires numerous inputs like year-specific payout ratios, growth rates, and betas, which can be challenging to estimate accurately for firms with uncertain financial forecasts. This complexity, combined with the model's high sensitivity to the firm's growth estimates and discount rate assumptions, can lead to significant inaccuracies in valuation, especially during transition and stable growth phases.
• Challenges in Defining Growth Phase Durations: Accurately determining the length of each growth phase, particularly the extraordinary growth phase and the transition period, is a major challenge. The valuation is highly sensitive to these durations, with errors potentially leading to significant misvaluations. This complexity arises from the difficulty in converting qualitative company assessments into precise timeframes.
• Oversimplification of Growth Transition: The assumption of a linear transition from high to stable growth in the model may not accurately reflect the complex, sometimes non-linear nature of real-world growth shifts. These changes can be influenced by unpredictable market and internal factors, challenging the model's linear growth assumption.
• Dividend-Centric Valuation and Forecasting Issues: The model's focus on dividends can result in valuation inaccuracies for companies that do not align dividends with earnings. This approach may undervalue firms that prefer reinvesting earnings over distributing dividends, not fully representing the company’s growth potential. Additionally, forecasting future dividend growth, particularly in the high growth stage, is complex, as these firms often prioritize reinvestment over substantial dividend payments.

In summary, the Three-Stage DDM is a versatile but complex tool for stock valuation, particularly for firms with intricate growth patterns. Its limitations include the need for multiple input estimations, challenges in determining growth phase lengths, assumptions of linear growth transitions, a dividend-centric approach that might not capture a company's entire value, challenges in predicting dividend growth, and sensitivity to risk and discount rate assumptions. Therefore, it's prudent to employ the Three-Stage DDM alongside other valuation methods, acknowledging its limitations for a more comprehensive assessment of a company's value.

Three-Stage Dividend Discount Model Example

For our example of valuing a dividend-paying company using the Three-Stage Dividend Discount Model (DDM), we'll use Home Depot (HD) as our case study. Home Depot is a leading American home improvement retailer, known for offering a wide range of products and services for construction, renovation, and home maintenance.

This is an appropriate company to use for the Three-Stage DDM due to several key reasons:

1. Strong Dividend Track Record Reflecting FCFE: Home Depot has a history of dividend payouts that closely align with its free cash flows to equity. The company's dividends have shown an average year-over-year growth of 15.5% over the last 5 years, demonstrating a strong and consistent dividend policy.
2. Stable Financial Leverage Indicating Consistent Financial Strategies: The company's stable financial leverage, with debt-to-asset ratios consistently between 60% to 75% over the past 5 years, indicates consistent financial strategies and capital structure, which is ideal for the Three-Stage DDM calculation.
3. High Dividend Growth With Expected Slowing: Home Depot’s dividend growth is relatively high, and considering its significant size and dominant market share, it's reasonable to anticipate that dividend growth will eventually slow down in line with the business lifecycle. This expectation fits well with the transitional phase of the Three-Stage DDM.

For applying the Three-Stage DDM to Home Depot, we'll utilize the more sophisticated valuation model formula (option #2), given its higher accuracy and alignment with the model's assumptions. This involves collecting the latest dividends per share (DPS₀) and earnings per share (EPS₀) figures, as well as locating/calculating the firm's current return on equity (ROE) and dividend payout ratio (DPR₁).

Estimating the return on equity and dividend payout ratio (DPR₂) in the stable growth phase is also necessary. We'll also estimate the initial extraordinary dividend growth rate (g₁) from Home Depot’s strong dividend growth, and the subsequent lower, stable growth rate (g₂) for the final phase. Further, we'll estimate the length of the extraordinary growth (n₁) and transition growth (n₂) phases.

Three discounts are also utilized in the Three-Stage DDM formula: r_e,1 for the extraordinary (in our case, high) growth phase, r_e,2 for the transition phase, and r_e,3 for the stable growth phase. These components enable a detailed valuation of Home Depot’s stock, capturing the nuances of its growth and financial profile.

Step #1: Dividends Per Share (DPS₀), Earnings Per Share (EPS₀), Dividend Payout Ratio (DPR₁), and Return on Equity (ROE)

The first step is to locate/calculate key information in the Three-Stage DDM formula, which includes the firm's current dividends per share (DPS₀), earnings per share (EPS₀), dividend payout ratio (DPR₁), and return on equity (ROE). This also provides us with a reference point for making estimates on the firm's future DPS, EPS, DPR, and ROE.

Dividends Per Share (DPS₀)

To start, we must identify the current dividend for Home Depot. Their latest financial statements or press releases, available on the investor relations section of their official website, are reliable sources for this information. Additionally, financial news websites and stock market analysis platforms regularly update dividend data for publicly traded companies like Home Depot. These sources will yield the initial dividends per share (DPS₀).

According to Home Depot's historical dividend information page, the company's 2023 annual dividend is $8.36, which will be our "DPS₀" in the Three-Stage DDM calculation.

Given the relationship between EPS and the DPR, you can also calculate the annual DPS as follows:

Annual Dividends Per Share (DPS) = Earnings Per Share (EPS) * Dividend Payout Ratio (DPR)

For instance, the EPS and DPR for Home Depot are $16.74 and 49.94% respectively (calculated and defined below), which means the firm's annual DPS is $8.36 ($16.74 * 49.94%). This is an important calculation and relationship to keep in mind given its relevance in the Three-Stage DDM.

Earnings Per Share (EPS₀)

Earnings per share (EPS) indicates the amount of a company's profit that is allocated to each outstanding share of common stock. This is typically found at the bottom of a company's income statement, but it can also be calculated as follows:

Earnings Per Share (EPS) = (Net Income - Preferred Dividends) / Weighted Average Shares Outstanding

If we use FY 2022 numbers, we can calculate the Home Depot's current earnings per share:

Earnings Per Share (EPS) [HD] = ($17,105M - $0M) / 1,022M --> $16.74

This $16.74 will therefore be our "EPS₀" in the Three-Stage DDM calculation.

Dividend Payout Ratio (DPR₁)

The dividend payout ratio (DPR) shows the percentage of a company's earnings that is distributed to shareholders in the form of dividends. It's a way to measure how much profit is being returned to shareholders as dividends compared to how much the company is retaining to reinvest in the business.

The dividend payout ratio formula is shown below:

Dividend Payout Ratio (DPR) = DPS / EPS

where:

• DPS = annual dividends per share
• EPS = earnings per share ((net income - preferred dividends) / weighted average shares outstanding)

This is calculated below for Home Depot, using the DPS and EPS numbers we've already identified from before:

Dividend Payout Ratio (DPR) [HD] = $8.36 / $16.74 --> 49.94%

This 49.94% will therefore be our "DPS₁" in the Three-Stage DDM calculation.

Return on Equity (ROE)

Return on equity (ROE) is a financial ratio that measures the profitability of a company in relation to shareholders' equity. It indicates how efficiently a company uses the money invested by shareholders to generate profits.

The return on equity formula is shown below:

Return on Equity (ROE) = Net Income / Shareholders' Equity

Here, net income is the profit a company earns after deducing all expenses, including taxes and interest. Shareholders' equity is the residual interests in the assets of the company after deducting liabilities. It represents the amount that shareholders would receive if the company's assets were liquidated and all debts were paid off.

For Home Depot, we can calculate ROE using their FY 2022 net income and shareholders' equity figures, which can be found in their financial statements:

Return on Equity (ROE) [HD] = $17,105M / $1,562 --> 10.95 or 1095.07%

Clearly, Home Depot's ROE of 1095.1% is very high, given the size of its net income relative to its shareholders' equity, which unfortunately makes it more challenging to accurately predict the firm's expected stable growth dividend payout ratio (DPR). We'll cover how to work around this when discussing the stable phase DPR₂ further below.

Step #2: Extraordinary Dividend Growth Rate (g₁)

To determine a company's extraordinary growth rate (g₁), it's common practice to evaluate the average growth rate during a previous period of high growth. This assessment may involve computing a simple average of the year-over-year growth rates or employing the compound annual growth rate (CAGR) for a time frame when the growth deviates from the norm or seems unsustainable and/or temporary. Another option is to estimate the "expected growth rate," which is calculated by multiplying the firm's current retention ratio and return on equity. We'll show all of these methods in this section.

For illustration purposes, I've collected dividend data for Home Depot from 2004 to 2023, as shown below:

Clearly, Home Depot has seen a long and consistent growth pattern in its dividends. Now, to find Home Depot's extraordinary growth rate (g₁) for the Three-Stage DDM, we'll begin by examining the firm's more recent growth rate. Besides a slight increase in 2022 (growth rate of 15.2%), Home Depot's dividends have consistently grown ~10% year-over-year in 2020, 2021, and 2023, thereby making 10% a reasonable assumption for the firm's high dividend growth rate.

Now, if we wanted to assess this growth over a longer period, the CAGR calculation is preferable.

For reference, the formula for CAGR is shown below:

CAGR = [(Ending Value / Beginning Value)^{(1 / Number of Years)}] - 1

We can calculate the CAGR to assess Home Depot's dividend growth over time. In our case, we'll show this over a 10-year period (2014 to 2023):

CAGR [HD] = [($8.36 / $1.88)^{(1 / 9)}] - 1 --> 18.03%

We can calculate the CAGR over various periods to observe changes over time. However, for simplicity, we'll use this 18% as our second estimation for the firm's high dividend growth rate

The next method for estimating growth is to calculate the expected growth rate, which measures a company's potential for growth using its own internally generated resources. This formula multiplies the retention ratio (the proportion of net income not paid out as dividends) by the return on equity (ROE) (how effectively a company uses shareholders' equity to generate profit). This approach indicates the level of growth that can be supported by retained earnings, without the need for external financing.

The expected growth rate formula is shown below:

Expected Growth Rate = Retention Ratio * Return on Equity

where:

• Retention ratio = 1 - dividend payout ratio (DPR). Dividend payout ratio = dividends per share (DPS) / earnings per share (EPS).
• Return on equity (ROE) = Net income / shareholders' equity

The expected growth rate is calculated below for Home Depot, using FY 2022 financial statement numbers:

Expected Growth Rate [HD] = (1 - ($8.36 / $16.74)) * ($17,105M / $1,562M) --> 50.06% * 1,095% --> 548.19%

It's evident that a 548.19% growth rate is exceptionally high and unrealistic for the company's first-stage dividend growth. This is primarily attributed to the firm's high ROE, which we have already noted. Nevertheless, this exceptionally high figure indicates that Home Depot is generating a significant level of profit relative to its shareholders' equity.

In conclusion, among the three methods we've used to estimate the firm's extraordinary growth rate (g₁), the 10% rate emerges as the most realistic and conservative choice. Therefore, we'll use this rate as our "g₁" in the Three-Stage DDM calculation.

Step #3: Perpetual Dividend Growth Rate (g₂)

To estimate the perpetual dividend growth rate (g₂), which predicts the indefinite increase of dividends, we'll briefly discuss the four methods commonly used by investors in dividend discount models (DDMs). Additionally, we'll explain why this rate should be below the nominal growth rate of the economy in which the firm operates.

• Related: How to Estimate the Perpetual Dividend Growth Rate in Dividend Discount Models

Four Methods of Estimating Perpetual Dividend Growth Rate

The four methods investors use to estimate the perpetual dividend growth rate in the Three-Stage DDM are briefly outlined and applied to Home Depot below:

1. Historical Dividend Growth Rates: This method bases the perpetual dividend growth rate on a firm's past dividend growth, analyzing data over an extended period (like 5+ years) for accuracy. While it provides a fundamental understanding of past trends, this approach may not fully account for future changes in the firm's financial health or market conditions​​. For Home Depot, this method would result in a high growth rate (near our extraordinary growth rate (g₁)), which is not suitable for a growth rate into perpetuity.
2. Sustainable Dividend Growth Rate: This approach calculates the growth rate based on a company's profitability (return on equity (ROE)) and the proportion of earnings paid out as dividends (dividend payout ratio (DPS / EPS)). It provides a realistic growth estimate by focusing on financial performance and is expressed as "ROE * (1 - (DPS / EPS))." Unfortunately, this approach doesn't work well for Home Depot, given its abnormally high ROE.
3. Augmented Sustainable Dividend Growth Rate: This method enhances the sustainable growth rate by including stock buybacks in the calculation, giving a more nuanced estimate by accounting for total shareholder returns (dividends plus buybacks). The formula to calculate the augmented dividend payout ratio is "(Dividends + Stock Buybacks - New Long Term Debt Issued) / Net Income))​." To calculate the actual growth rate, you'd then use the formula "ROE * (1 - Augmented Dividend Payout Ratio)." This approach offers a deeper insight into a company's financial activities, considering both dividends and buybacks, but necessitates careful evaluation of the firm's financial decisions. However, because this formula still relies on ROE for its calculation, for Home Depot it will still lead to an abnormally high perpetual dividend growth rate.
4. Future Dividend Growth Rate Analyst Estimates: This method relies on analysts' forecasts for future dividend growth, offering a quick but potentially less precise approach. The reliability of these estimates often decreases with longer projection periods and fewer analysts contributing to the consensus. While convenient, this approach should be used with an understanding of its limitations in accuracy​​. If we look to SeekingAlpha, currently 19 analysts are projecting the dividend to grow 5.73% in 2024, and 17 analysts are predicting 6.2% growth in 2025. However, these are near-term estimates and relying on analyst estimates is generally not the best approach.

Although none of these methods proved applicable or useful for Home Depot's case, this is not a concern. Adhering to the guideline discussed below is most important, as it is central to all DDMs.

Align Perpetual Dividend Growth With Economy's Growth Rate

In the Three-Stage DDM, the perpetual dividend growth rate (g₂) must be lower than the stable discount rate (r_e,3) to avoid unrealistic valuations. It should also not exceed the economy's growth rate where the firm operates. To ensure this, you can:

1. Cap at Economy's Growth Rate: Limit the dividend growth rate to the economy's growth rate where the firm operates, perhaps allowing a margin of 1-2% above this rate if justified by the model. This approach helps ensure that the growth rate remains realistic and aligned with the broader economic environment.
2. Risk-Free Rate as Benchmark: Use the 10-year U.S. Treasury Note interest rate as a conservative benchmark for the growth rate. This method provides a reference point grounded in a widely recognized and stable economic indicator, offering a safe estimate that minimizes the risk of overvaluation.
3. Combine Inflation and Economic Growth: Merge long-term inflation expectations with the average economic growth rate for a holistic approach. This method considers both the impact of inflation and economic expansion, offering a balanced perspective that factors in various macroeconomic variables.

These methods are standard in all dividend discount models (DDMs) to ensure a realistic growth rate, recognizing that no company can perpetually exceed the economy's growth or the risk-free rate.

For Home Depot, if we consider the 10-year breakeven inflation rate (the market's expected average inflation over the next 10 years), currently at 2.14%, and add it to the average 10-year GDP growth rate in the U.S. of 2.40%, we arrive at a rate of 4.54%. This indicates that Home Depot's perpetual growth rate should not exceed 4.54%. Given what we know of Home Depot's strong dividend growth rate, it's reasonable to assume their perpetual dividend growth rate (g₂) in the stable phase is 4.50%.

Step #4: Length of Extraordinary Growth (n₁) and Transition Growth Phases (n₂)

This section will discuss how to estimate the length of the extraordinary growth (n₁) and transition growth phases (n₂) in the Three-Stage DDM.

Length of Extraordinary Growth Phase (n₁)

Determining the length of the initial extraordinary growth phase in the Three-Stage DDM is subjective and requires a thorough analysis of the company's historical growth patterns, industry averages, competitive positioning, and future prospects. Investors typically assess factors such as historical earnings growth rates, industry life cycles, and the company’s specific strategic initiatives that could sustain or alter growth trends.

For a company like Home Depot, the duration of the extraordinary growth phase would be assessed by examining its past performance in revenue and earnings growth, market share expansion, and sector-specific trends like housing market health and consumer spending in home improvement. Factors such as Home Depot’s strategic plans, investments in growth areas, and potential market saturation, given its size and dominance, should also be considered.

To simplify our case, we observe that Home Depot has maintained a relatively high dividend growth rate over the past five years, with no evident signs of this trend diminishing in the near future. Additionally, the company maintains a moderate dividend payout ratio of ~50% and, as observed, a very high return on equity. These factors suggest that Home Depot is well-positioned to continue growing its dividends and efficiently generate income from its equity financing. Therefore, adopting an optimistic view of Home Depot's extraordinary growth period, we can assume it will maintain a high dividend growth rate of 10% for another 8 years before gradually transitioning to a perpetual dividend growth rate.

Length of Transition Growth Phase (n₂)

Determining the length of the transition growth phase in the Three-Stage DDM is as critical as identifying the duration of the initial extraordinary growth phase, although it remains largely subjective and challenging to estimate accurately. This phase acts as a bridge between the extraordinary growth rate (g₁) and the stable growth rate (g₂) and must be estimated with a balanced view of the company's potential for moderated growth.

For Home Depot, with a g₁ of 10% and an estimated g₂ of 4.5%, the length of the transition phase should be based on how quickly the company is expected to shift from its current high growth trajectory to the more sustainable growth rate. Key factors to consider include:

1. Market Maturation: Assess how close Home Depot is to reaching market saturation. As the company approaches this point, its growth is likely to slow down, signaling the start of the transition phase.
2. Industry Life Cycle: Consider where the home improvement sector stands in its life cycle. If the industry is maturing, this could indicate a shorter transition period as growth rates align more quickly with the broader market.
3. Strategic Initiatives Impact: Evaluate the expected impact of Home Depot's strategic initiatives on its growth rate. For instance, significant expansion or diversification plans could extend the high growth phase, whereas a shift towards consolidation might shorten it.
4. Economic and Market Conditions: Analyze broader economic trends, including housing market dynamics and consumer spending patterns, to gauge how external factors might influence the transition timeline.

Given Home Depot's robust growth and financial health, a gradual transition rather than an abrupt shift is reasonable to expect. A well-considered transition phase, perhaps spanning 6 years, may account for the company's current momentum while acknowledging the inevitability of growth normalization. This phase should be long enough to reflect a smooth and realistic deceleration in growth but not so prolonged as to ignore the imminent approach toward a more stable growth rate.

Step #5: Stable Growth Dividend Payout Ratio (DPR₂)

Following the assumptions of the Three-Stage DDM and the formula we're utilizing, a firm like Home Depot, which experiences an initial high growth rate followed by a declining growth rate and then transitions into an indefinite stable growth rate, is expected to have an initial low payout ratio during the high growth phase. This ratio is then followed by an increase during the transition phase, and finally, a high payout ratio in the stable growth phase.

Similarly, as ROE measures a company's profitability by assessing how efficiently it generates net income relative to its shareholders' equity, ROE might be elevated in the high-growth phase due to the benefits of reinvested earnings. However, it should decline in the transition phase and then normalize at a lower level in the stable growth phase. This shift in ROE indicates the company's transition to a more consistent growth trajectory.

One would estimate the payout ratio in stable growth by assuming a lower return on equity (ROE) for the firm in this phase. Estimating the firm's ROE, although not a required input in the Three-Stage DDM, can provide us with an estimate of the firm's dividend payout ratio (DPR) during the stable growth phase. This calculation is shown below:

Stable Dividend Payout Ratio (DPR) = 1 - (Stable Growth Rate (g₂) / Stable Return on Equity (ROE))

While the stable growth rate in this formula can be reasonable estimated, estimating the future ROE after the first stage and transition stage is more challenging, especially if the firm's ROE is as high as 1095%. In such cases you can consider one or more of the following methods to estimate the firm's stable DPR:

1. Disregard ROE, EPS, and DPR considerations and simply utilize the basic Three-Stage DDM formula.
2. Disregard ROE, EPS, and DPR considerations and simply grow the dividend by its extraordinary and perpetual dividend growth rates.
3. Use an average of past ROEs to smooth out the company's ROE (to calculate the stable DPR), although in Home Depot's case, this would still be relatively high.
4. Make an assumption about the stable growth DPR, largely ignoring the firm's ROE. This is the approach we'll adopt for Home Depot, as discussed below.

We'll use Home Depot's calculated DPR₁ of 49.9% as a starting point. Given our expectation for an increase in this rate as per the Three-Stage DDM model, we can project that DPR₂, following an 8-year period of extraordinary growth and a 6-year transitionary phase, may substantially rise, potentially reaching as high as 72.5%. This means that during the transition phase, the dividend payout ratio would gradually rise from 49.9% to 72.5% in linear increments.

Step #6: Discount Rates (r_e,1, r_e,2, r_e,3)

The discount rate (aka required rate of return), is primarily determined using the Capital Asset Pricing Model (CAPM). Fundamental in computing the present value of future cash flows in dividend discount models (DDMs), CAPM shows a direct link between the risk associated with an investment and its expected return. The model implies that with increased risks come higher returns. It's vital in determining the influence of market risks on the valuations of investments and their projected returns.

The CAPM formula is shown below:

r_e = r_f + β*(r_m - r_f)

where:

• R_e = cost of equity
• R_f = risk-free rate
• β = beta
• R_m = expected market return

Calculating the cost of equity (r_e) yields the discount rate needed for use in your present value DDMs.

Locating the three inputs to the CAPM for Home Depot is fairly straightforward:

• Risk-Free Rate (r_f): The risk-free rate is commonly represented by the yield on the 10-year U.S. Treasury Note, chosen for its reputation as one of the most secure investments. Guaranteed by the U.S. government, its risk of default is exceedingly low. This rate provides a critical baseline for comparing the risks of more speculative investments. Currently, this rate is at 4.18%.
• Beta (β): Beta evaluates the volatility of a stock relative to the overall market, signifying systematic risk, which pertains to the entire market or a market segment. A beta greater than 1 indicates more volatility compared to the market, while a beta less than 1 shows less volatility. Websites like Yahoo Finance provide beta values for companies, such as Home Depot, under "Beta 5Y Monthly." For instance, Home Depot's 5-year monthly beta is currently 0.94.
• Expected Market Return (r_m): The expected market return typically adopts a benchmark value of 10%, reflecting the long-term average annual return of broad market indices like the S&P 500. This figure is used as a general expectation for the market's average performance over a long duration.

Using these inputs, we can calculate the CAPM for Home Depot:

r_e,1 [HD] = 4.18% + 0.94*(10% - 4.18%) --> 9.65%

For Home Depot, a CAPM calculation yielding 9.65% represents the expected return on investment for the stock (aka "cost of equity"). This suggests that any investment in Home Depot should aim for at least this rate of return as compensation for the associated risks. In the context of the Three-Stage DDM model, this 9.65% is referred to as "r_e,1", denoting the discount rate used during the extraordinary growth phase.

• Related: How to Calculate and Interpret the Capital Asset Pricing Model (CAPM)

Now that we understand how to calculate the initial discount rate (r_e,1), the remaining task is to calculate or estimate the discount rate for the stable growth phase (r_e,3). This is because the discount rate for the transition period (r_e,2) will linearly decrease from r_e,1 in year 8 (the end of the extraordinary growth phase) to r_e,3 in year 6 (the conclusion of the transition phase).

To determine the cost of equity in the stable phase (r₃), the CAPM formula is still applicable. However, it's advisable to adjust the inputs of the CAPM to reflect the anticipated shifts in the company’s risk-return profile. Thus, the three components of the CAPM (r_m, r_f, and β) should be considered for these adjustments, as described below:

• Risk-Free Rate Adjustments: The risk-free rate, a macroeconomic factor, does not pertain to individual companies but instead mirrors broader economic conditions like monetary policies and inflation rates. Predicting changes in the risk-free rate is highly challenging due to its exposure to unpredictable economic and political events. This uncertainty emphasizes the need to base risk-free rate assessments in CAPM calculations on current and historical trends rather than speculative future changes, ensuring a realistic and well-founded cost of equity estimation.
• Beta Modification: Reassessing a company's beta, the measure of stock volatility relative to the market, is essential. As firms enter less risky and more predictable operations in the stable phase, a lower beta, usually between 0.8 to 1.2 for stable companies, is typically suitable. This lower beta indicates decreased volatility and implied risk, reducing the cost of equity. Conversely, should a company face greater market volatility or adopt riskier strategies, a higher beta would be justified, thereby increasing the cost of equity. This adjustment ensures the CAPM calculation accurately mirrors the company’s risk profile in its stable growth phase.
• Market Return Expectation Changes: Shifts in market return expectations, influenced by evolving market conditions or economic outlooks, can significantly affect the cost of equity. A decline in anticipated market returns, potentially due to a bearish outlook or reduced economic growth, would result in a lower cost of equity. In contrast, an uptick in expected market returns, reflecting more robust market growth, would elevate the cost of equity.

Therefore, in adjusting the CAPM for Home Depot's stable phase, one might reasonably estimate the beta to decrease to 0.84 (from its current 0.94). This adjusted beta would then be used to recalculate the CAPM, resulting in a cost of equity figure (r_e,3​) for the stable growth phase.

If we calculate the CAPM for the stable growth phase using this new estimated beta, it would be as follows:

r_e,3 [HD] = 4.18% + 0.84*(10% - 4.18%) --> 9.07%

The stable growth phase cost of equity for Home Depot, calculated using the CAPM, is 9.07%. This 9.07% figure is then utilized as the "r_e,3" input for the Three-Stage DDM calculation. Further, this also means that the transition period discount rate (r_e,2) will decline linearly from 9.65% (r_e,1) in year 8 (end of extraordinary growth phase) to 9.07% (r_e,3) in year 6 (end of transition phase), as mentioned prior.

One final note to consider is that the CAPM, while commonly used for calculating the discount rate in the Three-Stage DDM, is not the exclusive method. Alternatives, such as adopting your own required rate of return for the company, can provide additional insights. These varied approaches help to cross-verify and deepen the understanding of a company's risk-return profile.

Step #7: Calculate and Interpret the Three-Stage DDM

Now that we have all the inputs, we can calculate the Three-Stage DDM for Home Depot (HD). To simplify this calculation, we'll break it down into three stages: extraordinary growth, transition growth, and stable growth, and then sum the results to get our answer. It's best to calculate this using an Excel model, as solving it by hand or with a calculator can be a very lengthy process.

You can use the Three-Stage DDM Excel model attached below. This is a sophisticated model which allows for the use of high/low/negative growth rates in the first stage, modifications between how dividends are calculated, and more:

Note: This version is locked, restricting editing/viewing of locked cells except for the input cells. For the full version, please contact me.

Present Value of Extraordinary Growth Phase

Let's begin by calculating the present value (PV) of extraordinary growth. The table below shows how this should be output:

As you can see from the table above, the DPS & EPS growth rate, DPR₁, and discount rate (r_e,1) remain constant throughout the initial extraordinary growth phase for 8 years. The DPS and EPS grow by 10% every year, and the DPS can also be calculated by multiplying the EPS by the DPR. The PV of first-stage dividends for each year is calculated by dividing the expected dividends by one plus the discount rate raised to the power of the number of periods.

For example, here's the year 3 present value of dividends calculation for Home Depot:

PV₀ Year 3 Dividend [HD] = $11.13 / (1 + 0.096)³ --> $8.45

Summing the PV calculation for each year of the first-stage dividends (the last row of the table above) gives us $67.91.

Present Value of Transition Growth Phase

Next, let's calculate the present value (PV) of transition growth. The table below shows how this should be output:

Unlike the first stage, the DPS & EPS growth rate and the discount rate (r_e,2) both decline linearly over the 6-year transition period, while the DPR grows linearly over the same period (from DPR₁ to DPR₂). The DPS and EPS continue to grow by the DPS & EPS growth rate every year, and the DPS can still also be calculated by multiplying the EPS by the DPR. In this stage, because the discount rate changes every year, the present value calculation must use the cumulated cost of equity method.

For example, here's the year 11 present value of dividends calculation for Home Depot:

PV₀ Year 11 Dividend [HD] = $27.80 / ((1 + 0.096)⁸ * (1 + 0.0953) * (1 + 0.0944) * (1 + 0.0935)) --> $10.17

Summing the PV calculation for each year, but this time for the transition stage dividends (the last row of the table above), gives us $61.16.

Present Value of Stable Growth Phase

Finally, we can calculate the present value (PV) of stable growth into perpetuity. It's not possible to show this in table format (because the period length is indefinite), but here's what the next 10 years would look like:

Similar to the first stage, the DPS & EPS growth rate, DPR₂, and discount rate (r_e,3) remain constant through the stable growth period into perpetuity. The DPS and EPS grow by 10% every year, and as before, the DPS can also be calculated by multiplying the EPS by the DPR.

The PV of the terminal price would be calculated using the following formula (this is just the last part of the Three-Stage DDM formula):

Here's how this calculation would look for Home Depot, excluding the PV discounting "(1 + r_e)ⁿ":

This terminal price of $881.43 now has to be discounted back by "(1 + r_e)ⁿ." In other words, we must calculate the present value of this terminal price at the end of the transition phase to account for the time value of money, which involves dividing $881.43 by the initial discount rate (r_e,1) and every single calculated discount rate for every applicable year in the transition period.

This calculation is shown below for Home Depot:

Performing this calculation will provide you with a PV for the stable growth phase of $247.76.

Calculate Three-Stage DDM and Interpret Results

If we sum the present value of the extraordinary growth phase, transition growth phase, and stable growth phase, we'll get $376.83 ($67.91 + $61.16 + $247.76) as our fair/intrinsic value (P₀) for Home Depot. Also, if we were to plot the company's DPS, and DPS & EPS growth rate from 2024 to 2047, here's what it would look like:

Now, in terms of interpretation, the Three-Stage DDM places Home Depot's intrinsic value at $376.83, in contrast to its current market price of ~$326.47. This indicates potential undervaluation, as the market price is less than the calculated intrinsic value.

Additionally, implementing a 15% margin of safety, a prudent measure considering the inherent uncertainties in both the model and the company's context, helps ascertain a more realistic buying price. This conservative approach adjusts the buying price to $320.31 ($376.83 * (1 - 0.15)). Consequently, the stock now appears slightly overvalued, as it is slightly below the company's current market price.

Finally, given the Three-Stage Model's reliance on specific input variables and assumptions, a sensitivity analysis is crucial for accurate valuation. Using an iterative data table is an efficient approach, providing insight into how minor variations in two critical inputs of the model affect outcomes. For this analysis, we'll explore the impact of small changes, specifically a 0.5% alteration in the perpetual dividend growth rate (4.5%) and a 2.5% adjustment in the margin of safety (15%), on Home Depot's buy price.

Below is the iterative data table, illustrating the effect of these minor adjustments on Home Depot's buy price:

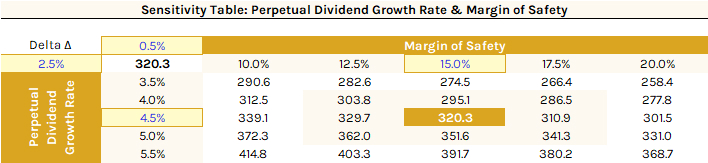
Ultimately, the process of executing a sensitivity analysis, as shown above, highlights the vital role of key inputs in the Three-Stage DDM. These include the judicious selection of the target company, accurate calculation of discount rates, informed estimations of dividend growth rates and payout ratios across different stages, and the adoption of a sensible margin of safety. These components significantly affect our understanding of a company's valuation. Therefore, this comprehensive approach is highly recommended for the accurate implementation of the Three-Stage DDM.

The Bottom Line

The Three-Stage Dividend Discount Model (DDM) represents a sophisticated approach in the realm of stock valuation, adeptly capturing the nuanced growth trajectory of a company through three distinct phases: an initial period of extraordinary growth, a transitional phase where growth rates either linearly decline or increase, and finally a stable growth phase extending into perpetuity. This model is particularly suitable for companies navigating through various stages of their lifecycle, offering a dynamic perspective that aligns with the evolving nature of business growth.

However, the Three-Stage DDM is not without its complexities and limitations. It requires careful consideration of multiple factors including the accurate estimation of growth rates, dividend payout ratios, and discount rates across different growth stages. These estimations, inherently uncertain due to the fluctuating nature of markets and company-specific dynamics, present a significant challenge. Additionally, the model's assumption of linear transitions between growth stages may oversimplify the intricate realities of business evolution.

Despite these challenges, the Three-Stage DDM remains an invaluable tool in the investor's toolkit. It offers a more comprehensive view compared to simpler models (like the Gordon Growth Model (GGM)), especially for companies experiencing significant shifts in their growth patterns. By incorporating varying growth rates and dividend payout ratios throughout a company's lifecycle, it provides a more detailed and realistic assessment of a stock's intrinsic value. When used judiciously, alongside other valuation methods and market analyses, the Three-Stage DDM can be instrumental in identifying potential long-term investment opportunities, helping investors discern between overvalued and undervalued dividend-paying stocks.